Tabella dei Contenuti
Nel mondo della Data Science, l’attenzione è quasi interamente focalizzata sul miglioramento dell’accuratezza del modello, relegando l’efficienza a una preoccupazione secondaria.
Tuttavia, quando un algoritmo esce dall'ambiente di prototipazione ed entra nell'ambiente di produzione per rispondere in tempo reale alle richieste degli utenti, le sue dimensioni e la ridotta velocità d'esecuzione si trasformano rapidamente in problemi concreti di performance.
Per affrontare questo divario tra accuratezza ed efficienza, la compressione dei modelli è emersa come una disciplina fondamentale: l'obiettivo è ridurre il numero di parametri e i requisiti computazionali senza sacrificare significativamente le prestazioni.
Questo articolo si propone come una guida pratica e approfondita per bilanciare accuratezza ed efficienza nell'intelligenza artificiale in produzione, esplorando le metriche di runtime essenziali che affiancano l'accuratezza.
- Knowledge Distillation (Distillazione della Conoscenza)
- Pruning (Potatura)
- Low-Rank Factorization (Fattorizzazione a Basso Rango)
- Quantization (Quantizzazione)
Iniziamo.
Motivazioni per la model compression
Nel campo del Machine Learning c’è una continua corsa a costruire modelli sempre più profondi: architetture con milioni di parametri promettono prestazioni di punta nei benchmark. Purtroppo, la maggior parte delle competizioni online tende a premiare la massima precisione e a trascurare aspetti come peso del modello, tempi di risposta e costi di deployment.
In ambienti reali, invece, un algoritmo deve rispondere velocemente e con un uso ragionevole di memoria e potenza di calcolo. Questo cambiamento di prospettiva rende evidente che spesso un modello "troppo accurato" è anche inutilizzabile se rende il sistema lento o troppo costoso da mantenere.
Quando un sistema va in produzione deve rispettare vincoli hardware e fornire risposte in tempi ragionevoli. Latenza, throughput e footprint in memoria diventano parametri altrettanto importanti rispetto alla sola accuratezza.
Vedremo a breve nel dettaglio come questi indicatori siano importanti nel definire una strategia di ottimizzazione dei nostri sistemi.
Ad esempio, per un assistente vocale o un sistema di raccomandazione bisogna garantire risposte quasi istantanee - l’utente non accetterà mai di aspettare secondi, o addirittura minuti, per una predizione.
Oltre alla soddisfazione dell’utente, l’efficienza incide direttamente sui costi infrastrutturali. Model compression significa poter gestire più richieste con lo stesso hardware oppure usare hardware più economico.
Nei sistemi distribuiti, modelli più piccoli si replicano facilmente su più server e permettono di scalare in modo elastico con il traffico. Su dispositivi edge o mobili, ridurre dimensioni e consumo energetico è indispensabile affinché l’IA funzioni offline.
Metriche operative da considerare in produzione
Il processo di valutazione per un algoritmo di machine learning in generale, è volto a valutare se l'algoritmo è adatto al mondo reale, deve prendere in considerazione indicatori che non sono rivolti solo all'accuratezza del modello in accezione generale ma deve valutare anche altri aspetti che hanno un forte impatto in termini di fruibilità del servizio.
Tra gli indicatori più importanti troviamo:
- Latenza in inferenza
- Throughput
- Dimensione del modello
Latenza in inferenza
La latenza è il tempo impiegato da un modello per ricevere un input, elaborarlo e produrre l’output. In un’analisi quantitativa, la latenza può essere scomposta in due componenti:
- Il tempo necessario per eseguire le operazioni aritmetiche \(T_{\text{compute}}\)
- Il tempo per trasferire i dati dalla memoria al processore \(T_{\text{memory}}\)
La formula spesso utilizzata per stimare la latenza è latency = max(T_memory, T_compute). Ridurre la dimensione delle matrici di pesi o usare rappresentazioni a precisione ridotta riduce sia il numero di operazioni che la quantità di dati da trasferire, migliorando direttamente la latenza
Throughput
Il throughput misura quante predizioni al secondo un modello è in grado di servire. A differenza della latenza, il throughput dipende dal numero di richieste simultanee e dall’efficienza con cui vengono eseguite in batch.
Riducendo la complessità del modello possiamo elaborare più richieste contemporaneamente, aumentando il numero di inferenze per unità di tempo
Dimensione del modello
Il footprint in memoria è la quantità di memoria necessaria per caricare e far girare un modello. Questa grandezza è determinata principalmente dal numero di parametri e dal tipo di dato utilizzato per rappresentarli.
Ad esempio, se tutti i pesi vengono rappresentati con variabili a 32 bit (float32), l’occupazione di memoria sarà quadrupla rispetto a una rappresentazione a 8 bit. La compressione agisce su questo fronte riducendo il numero di parametri o diminuendo il numero di bit necessari per rappresentarli
- Latenza: tempo end-to-end per completare una singola inferenza (tipico: ms), dal dato in ingresso all’output del modello.
- Throughput: numero di inferenze completate per unità di tempo (tipico: esempi/s), dipende da batch size, parallelismo e I/O.
- Footprint in memoria: quantità di RAM/VRAM occupata da modello, pesi, attivazioni, buffer e runtime durante training/inferenza (picco rilevante).
Caso studio reale: "Netflix Prize"
La storia del Netflix Prize è un monito fondamentale nel mondo della Data Science. Nel 2006, Netflix lanciò una competizione pubblica con un premio di un milione di dollari per chi fosse riuscito a migliorare del 10% il suo algoritmo di raccomandazione. Sebbene un team abbia raggiunto l'obiettivo vincendo il premio nel 2009, quel modello non fu mai utilizzato in produzione.
Il motivo? Non la scarsa accuratezza, ma l'eccessiva complessità. Netflix dichiarò che i lievi guadagni in precisione non giustificavano lo sforzo di ingegnerizzazione richiesto per l'implementazione. Il modello vincente era troppo oneroso e lento per essere eseguito in tempo reale su milioni di utenti, rendendo il sistema insostenibilmente costoso.
Netflix scelse una soluzione più semplice ed efficiente, dimostrando che, in un ambiente di produzione reale, una piccola perdita di accuratezza può essere un compromesso accettabile a fronte di grandi risparmi in termini di costi e latenza.
Tecniche di compressione dei modelli
La compressione dei modelli comprende diverse tecniche che hanno l’obiettivo di ridurre dimensioni e complessità computazionale di un algoritmo senza comprometterne (troppo) la capacità predittiva. I benefici attesi sono molteplici: diminuzione della latenza, diminuzione del consumo di memoria, maggiore facilità di scalare il servizio e, in alcuni casi, anche una miglior generalizzazione. Le quattro strategie più diffuse sono:
- Knowledge Distillation
- Pruning
- Low-Rank Factorization
- Quantization
Knowledge Distillation
La distillazione della conoscenza è una tecnica introdotta da Hinton et al. per trasferire le competenze di un modello grande (teacher) in un modello più piccolo (student). Il modello studente viene addestrato non solo sui dati originali ma anche sulle soft probabilities emesse dal teacher, l’obiettivo è imitare la distribuzione delle probabilità del maestro e quindi riprodurne il comportamento. La distillazione può essere applicata a classificazione, regressione e persino a modelli generativi.
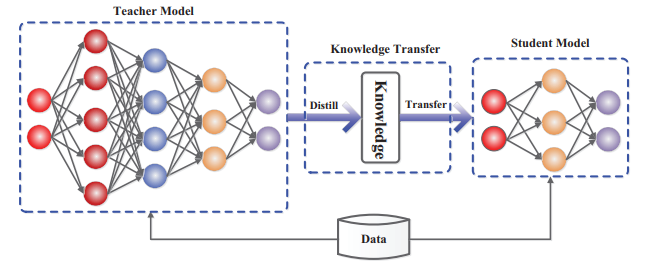
Un esempio emblematico è DistilBERT, versione compressa di BERT per il linguaggio naturale. Secondo un’analisi recente di Zilliz (settembre 2024), DistilBERT mantiene circa il 97 % della capacità di comprensione del linguaggio di BERT, pur essendo più piccolo del 40 % e più veloce del 60 % nelle operazioni di inferenza. Su dispositivi mobili, l’inferenza risulta addirittura più rapida del 71 %. Questi risultati mostrano come un modello distillato possa offrire un ottimo compromesso tra accuratezza e velocità.
Quindi nella pratica che cos'è la "Distillazione della Conscenza"? Il termine può essere scomposto come segue:
- Conoscenza (Knowledge): In questo contesto, si riferisce alla comprensione, agli insight e alle informazioni che un modello di machine learning ha acquisito durante l'addestramento. Questa "conoscenza" è tipicamente rappresentata dai parametri del modello, dai pattern appresi e dalla sua capacità di fare previsioni.
- Distillazione (Distillation): Significa trasferire o condensare questa conoscenza da un modello all'altro. Questo processo prevede di addestrare il modello student affinché ne mimi il comportamento del modello teacher, trasferendo così efficacemente gli insight appresi.
Si tratta essenzialmente di un processo in due fasi:
- Si addestra il modello grande (ad esempio, un'architettura complessa e lenta) in modo standard. Questo è il modello "teacher" (maestro).
- Si addestra un modello più piccolo e leggero, destinato a imitare il comportamento del modello più grande. Questo è il modello "student" (studente).
L'obiettivo principale della distillazione della conoscenza è proprio trasferire gli insight appresi dal teacher allo student. Ciò consente al modello student di raggiungere prestazioni paragonabili con un numero drasticamente inferiore di parametri e una ridotta complessità computazionale.
Il concetto ha un senso intuitivo: proprio come in un contesto accademico, il modello student potrebbe non eguagliare perfettamente le prestazioni del teacher, ma con un addestramento coerente, è possibile creare un modello più piccolo che sia quasi altrettanto performante del suo omologo più grande, ma molto più efficiente in produzione.
Pruning
La Potatura (Pruning) è una tecnica di compressione che consiste nell’eliminare (azzerare) pesi, neuroni o interi filter che contribuiscono in misura marginale alla capacità predittiva del modello. L'obiettivo è creare una rete più snella e veloce sfruttando la naturale "sovraparametrizzazione" dei modelli di deep learning.
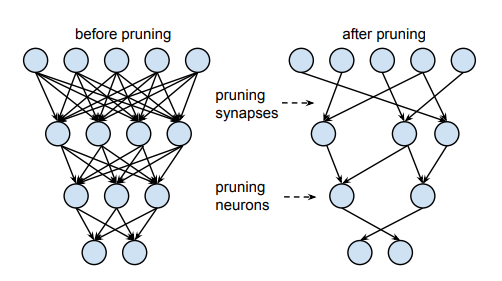
Le strategie principali si differenziano in base all'elemento che viene rimosso:
1. Pruning Non Strutturato (o Weight Pruning)
Questa è la forma più granulare: si rimuovono i singoli collegamenti (pesi) il cui valore assoluto è molto vicino allo zero, considerandoli ridondanti.
- Vantaggi: Offre la massima compressione in termini di parametri. Se i pesi residui sono memorizzati come matrici sparse, si riduce notevolmente lo spazio di memoria richiesto.
- Nota: Ricerche come quella di Han et al. dimostrano che cicli iterativi di addestramento e potatura possono eliminare una parte significativa delle connessioni mantenendo quasi inalterata l'accuratezza. Tuttavia, per ottenere un reale guadagno in velocità di inferenza, è spesso necessario un hardware specializzato che acceleri le operazioni sulle matrici sparse.
2. Pruning Strutturato (o Unit Pruning)
Questa strategia rimuove intere unità funzionali (neuroni, canali di convoluzione o strati completi). La topologia della rete viene modificata, riducendo drasticamente il numero di operazioni di moltiplicazione e accumulazione.
- Vantaggi: Ha un impatto maggiore sulla dimensione del modello e, crucialmente, velocizza la rete sui device standard poiché elimina la necessità di eseguire calcoli inutili.
- Sfida: La rimozione è più aggressiva. Richiede cautela nel selezionare le unità da eliminare, basandosi su metriche di importanza specifiche per evitare un degrado significativo dell'accuratezza.
Altre Strategie
Esistono varianti che affinano la selezione degli elementi da potare:
- Pruning basato sull’Attivazione: Analizza le attivazioni dei neuroni sui dati di training e rimuove quelli che rimangono costantemente "spenti" (o inattivi), individuando efficacemente le ridondanze a livello di neurone.
- Pruning basato sulla Ridondanza: Identifica e rimuove neuroni che, pur essendo attivi, mostrano risposte eccessivamente simili all'interno dello stesso strato, suggerendo una duplicazione della funzione.
L’approccio di potatura non è un’azione isolata. Se combinato con altre tecniche come la Quantizzazione, si possono ottenere risultati impressionanti:
- Un pruning intelligente su AlexNet ha ridotto il modello di 9 volte, rendendolo circa 3 volte più veloce. Abbinandolo alla quantizzazione, la riduzione totale ha raggiunto un fattore di 35 volte.
- Su VGG16, il solo pruning ha comportato una riduzione di 13 volte, che è salita a ben 49 volte con l'aggiunta della quantizzazione.
Questi risultati dimostrano che la potatura è uno strumento potente per la miniaturizzazione dei modelli e, in combinazione, può sbloccare livelli di efficienza cruciali per l'implementazione in edge computing e su larga scala.
Low-Rank Factorization
Molte reti neurali, in particolare i modelli complessi, utilizzano grandi matrici di pesi che sono spesso sovraparametrizzate, implicando che gran parte della loro informazione (o rango effettivo) è ridondante. La Fattorizzazione a Basso Rango è una tecnica che sfrutta questo concetto per comprimere il modello, approssimando la matrice di peso originale con il prodotto di due o più matrici più piccole.
Questa operazione si basa sul principio che non tutte le "direzioni" nello spazio dei pesi sono essenziali per rappresentare le trasformazioni apprese. Di conseguenza, la matrice originale può essere approssimata da una matrice con un rango inferiore (k) senza una significativa perdita d’informazione.
Tecniche classiche come la Scomposizione a Valori Singolari (SVD) o la decomposizione di Tucker scompongono la grande matrice di peso W nei suoi fattori (U,S,V). Scegliendo attentamente il rango k (il numero di valori singolari da mantenere), si ottiene un preciso compromesso tra la riduzione dei parametri e la fedeltà del modello compresso.
Una matrice dei pesi W, di dimensioni m × n e rango r, può essere decomposta in matrici più piccole utilizzando la decomposizione ai valori singolari (SVD), come illustrato nella figura seguente.
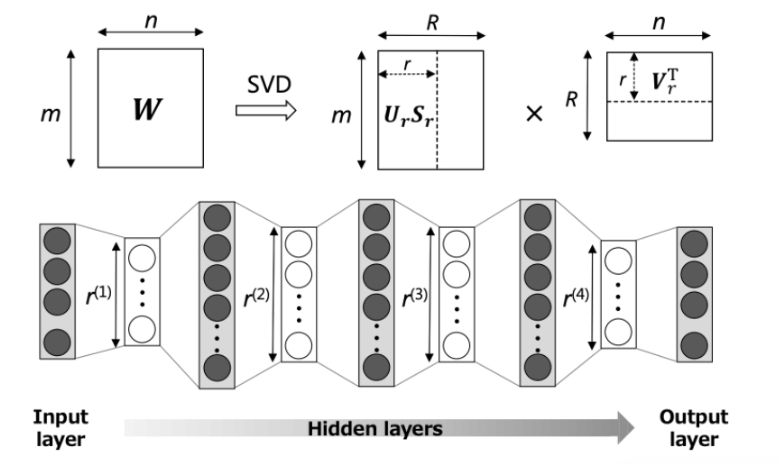
Secondo diverse panoramiche sulle tecniche di compressione, l'applicazione della Fattorizzazione a Basso Rango può portare a una riduzione del modello e a un miglioramento della velocità di inferenza del 30-50% sugli strati densi (Fully Connected).
Tuttavia, è importante notare che la decomposizione introduce un costo computazionale aggiuntivo durante l’addestramento (o il fine-tuning post-decomposizione) e che il rango ottimale deve essere individuato empiricamente per ogni architettura specifica.
Quantization
La Quantizzazione è una tecnica fondamentale che riduce la precisione numerica utilizzata per rappresentare sia i pesi che le attivazioni del modello. Tipicamente, i pesi di un modello vengono addestrati e memorizzati in virgola mobile a 32 bit (FP32); la quantizzazione mira a ridurli a formati a bassa precisione, come 16 bit (FP16), 8 bit (INT8) o, in alcuni casi estremi, a 4 o persino 1 bit.
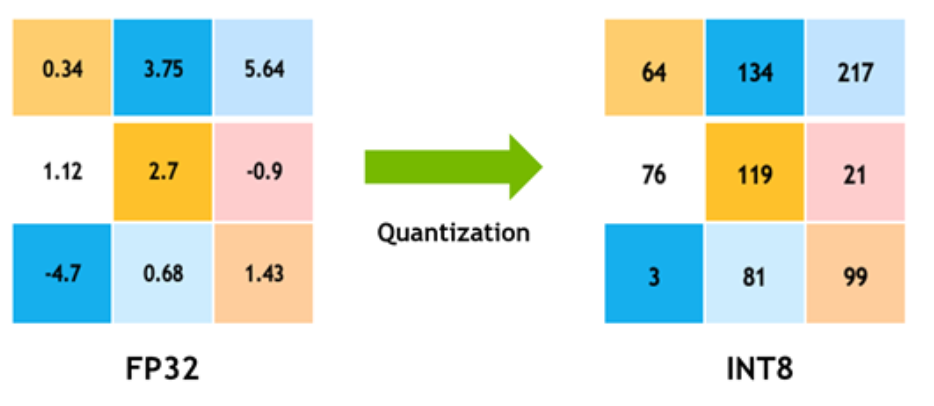
Questa mappatura da FP32 a interi a bassa precisione comprime notevolmente i valori e, di conseguenza, la memoria utilizzata. Il vantaggio cruciale è che i processori e l'hardware specializzato (come le unità AI) possono eseguire le operazioni su dati a precisione ridotta in modo significativamente più rapido ed efficiente, abbattendo i tempi di inferenza.
Le due modalità principali per implementare la quantizzazione sono:
1. Quantizzazione Post-Training (PTQ)
In questa modalità, il modello viene prima addestrato interamente a precisione piena (FP32). Solo in un secondo momento, dopo l'addestramento, i pesi vengono convertiti alla precisione inferiore (ad esempio, INT8).
- Pro: È la più rapida da implementare, non richiede tempo aggiuntivo di training.
- Contro: Nonostante i miglioramenti in velocità e riduzione della memoria, la conversione a posteriori può causare una perdita di accuratezza (o precisione) dovuta agli errori di arrotondamento.
2. Quantizzazione Consapevole dell'Addestramento (Quantization-Aware Training - QAT)
In questo approccio, la logica della quantizzazione viene simulata durante l'intero processo di training o fine-tuning. Il modello impara quindi ad adattarsi alle limitazioni di precisione che saranno presenti in produzione.
- Pro: Offre modelli più accurati rispetto alla PTQ, poiché il modello si addestra già tenendo conto degli effetti dell'arrotondamento.
- Contro: Richiede un tempo di training aggiuntivo per simulare e integrare il processo di quantizzazione.
La combinazione della quantizzazione con il pruning ha dimostrato un'efficacia straordinaria: ad esempio, il binomio pruning + quantization su AlexNet ha ridotto la dimensione del modello di ben 35 volte, mentre su VGG16 la riduzione ha raggiunto un impressionante fattore di 49 volte, rendendo questi modelli utilizzabili in scenari edge o a bassissimo consumo energetico.
Implementazione Pratica delle Tecniche di Compressione
Questa sezione presenta l'implementazione dettagliata delle quattro principali tecniche di compressione dei modelli utilizzando PyTorch e il dataset MNIST come caso di studio. Ogni tecnica viene illustrata con codice funzionale, spiegazioni approfondite e risultati quantitativi.
Setup Iniziale
Prima di iniziare con le tecniche di compressione, è necessario preparare l'ambiente e caricare il dataset. Il setup include l'importazione delle librerie necessarie e la configurazione dei dataloader:
import sys
import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import torch.nn.functional as F
import numpy as np
import pandas as pd
from time import time
from tqdm import tqdm
from torch.utils.data import DataLoader
Il dataset MNIST viene caricato con normalizzazione appropriata. I valori di normalizzazione (0.1307, 0.3081) rappresentano rispettivamente la media e la deviazione standard del dataset MNIST:
transform = transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])
trainset = torchvision.datasets.MNIST(root='./data', train=True,
download=True, transform=transform)
trainloader = DataLoader(trainset, batch_size=64, shuffle=True)
testset = torchvision.datasets.MNIST(root='./data', train=False,
download=True, transform=transform)
testloader = DataLoader(testset, batch_size=64, shuffle=False)
Definiamo una funzione di valutazione che sarà riutilizzata per tutte le tecniche:
def evaluate(model):
model.eval()
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
inputs, labels = data
outputs = model(inputs)
_, predicted = torch.max(outputs.data, 1)
total += labels.size(0)
correct += (predicted == labels).sum().item()
return correct / total
Knowledge Distillation
La distillazione della conoscenza è una tecnica elegante che permette di trasferire le capacità di un modello complesso (teacher) a uno più leggero (student) attraverso l'imitazione delle distribuzioni di probabilità. Invece di imparare solo dalle etichette corrette (hard labels), lo student impara dalle "soft probabilities" del teacher, che contengono informazioni più ricche sulle relazioni tra le classi.
Architettura del Teacher Model
Il teacher è un modello convoluzionale con circa 70.000 parametri che include strati di convoluzione, pooling e fully connected:
class TeacherNet(nn.Module):
def __init__(self):
super(TeacherNet, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 5) # 32 filtri convoluzionali 5x5
self.pool = nn.MaxPool2d(5, 5) # Max pooling 5x5
self.fc1 = nn.Linear(32 * 4 * 4, 128) # Layer fully connected
self.fc2 = nn.Linear(128, 10) # Output layer (10 classi)
def forward(self, x):
x = F.relu(self.conv1(x))
x = self.pool(x)
x = x.view(x.size(0), -1)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
Il training del teacher segue l'approccio standard di classificazione con cross-entropy loss:
teacher_model = TeacherNet()
teacher_optimizer = optim.Adam(teacher_model.parameters(), lr=0.001)
teacher_criterion = nn.CrossEntropyLoss()
for epoch in range(5):
teacher_model.train()
running_loss = 0.0
for data in trainloader:
inputs, labels = data
teacher_optimizer.zero_grad()
outputs = teacher_model(inputs)
loss = teacher_criterion(outputs, labels)
loss.backward()
teacher_optimizer.step()
running_loss += loss.item()
teacher_accuracy = evaluate(teacher_model)
print(f"Epoch {epoch + 1}, Loss: {running_loss / len(trainloader)}, "
f"Accuracy: {teacher_accuracy * 100:.2f}%")
Il teacher model raggiunge rapidamente un'accuratezza elevata, attestandosi al 98.79% dopo 5 epoche.
Architettura dello Student Model
Lo student utilizza esclusivamente layer fully connected, eliminando completamente gli strati convoluzionali. Questa scelta architetturale riduce drasticamente sia il numero di parametri che la complessità computazionale:
class StudentNet(nn.Module):
def __init__(self):
super(StudentNet, self).__init__()
self.fc1 = nn.Linear(28 * 28, 128) # Input diretto dalle immagini appiattite
self.fc2 = nn.Linear(128, 10) # Output layer
def forward(self, x):
x = x.view(x.size(0), -1) # Appiattisce l'immagine 28x28 in vettore 784
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
Training con Knowledge Distillation
La funzione di loss è il cuore della distillazione. Utilizza la divergenza di Kullback-Leibler (KL) per misurare quanto le distribuzioni di probabilità dello student divergono da quelle del teacher. La KL divergence penalizza lo student quando le sue predizioni si allontanano da quelle del teacher:
def knowledge_distillation_loss(student_logits, teacher_logits):
p_teacher = F.softmax(teacher_logits, dim=1) # Probabilità teacher
p_student = F.log_softmax(student_logits, dim=1) # Log-probabilità student
loss = F.kl_div(p_student, p_teacher, reduction='batchmean')
return loss
Il processo di training dello student è diverso dal training standard. Non usiamo le etichette vere, ma le predizioni del teacher:
student_model = StudentNet()
student_optimizer = optim.Adam(student_model.parameters(), lr=0.001)
for epoch in range(5):
student_model.train()
running_loss = 0.0
for data in trainloader:
inputs, labels = data
student_optimizer.zero_grad()
student_logits = student_model(inputs)
# Detach per evitare backpropagation attraverso il teacher
teacher_logits = teacher_model(inputs).detach()
loss = knowledge_distillation_loss(student_logits, teacher_logits)
loss.backward()
student_optimizer.step()
running_loss += loss.item()
student_accuracy = evaluate(student_model)
print(f"Epoch {epoch + 1}, Loss: {running_loss / len(testloader)}, "
f"Accuracy: {student_accuracy * 100:.2f}%")
Risultati e Confronto
I risultati dimostrano l'efficacia della distillazione:
- Teacher Model: 98.79% accuratezza, tempo di inferenza 729 ms ± 21.4 ms
- Student Model: 96.33% accuratezza, tempo di inferenza 627 ms ± 16.9 ms
Lo student mantiene il 97.5% delle performance del teacher con un'architettura molto più semplice e un'inferenza circa 14% più veloce. Questo dimostra che la conoscenza implicita nelle soft probabilities è molto più informativa delle semplici etichette binarie.
Pruning (Potatura)
Il pruning sfrutta il fatto che molte reti neurali sono sovraparametrizzate: gran parte dei loro pesi contribuiscono marginalmente alla capacità predittiva. Eliminando questi pesi ridondanti, possiamo ottenere modelli più compatti senza perdite significative di accuratezza.
Modello Base
Utilizziamo una rete fully connected con quattro layer per un totale di 566,528 parametri di peso:
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__()
self.fc1 = nn.Linear(28 * 28, 512) # 401,920 parametri
self.fc2 = nn.Linear(512, 256) # 131,072 parametri
self.fc3 = nn.Linear(256, 128) # 32,768 parametri
self.fc4 = nn.Linear(128, 10) # 1,280 parametri
def forward(self, x):
x = x.view(x.size(0), -1)
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
x = torch.relu(self.fc3(x))
x = self.fc4(x)
return x
Training standard del modello con Adam optimizer e cross-entropy loss:
net = SimpleNet()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), lr=0.001)
for epoch in range(5):
running_loss = 0.0
net.train()
for data in trainloader:
inputs, labels = data
optimizer.zero_grad()
outputs = net(inputs.view(-1, 28*28))
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
accuracy = evaluate(net)
print(f"Epoch {epoch + 1}, Loss: {running_loss / len(trainloader)}, "
f"Accuracy: {accuracy * 100:.2f}%")
torch.save(net, "net.pt")
Definizione della Soglia e Applicazione del Pruning
Il zero-pruning elimina tutti i pesi il cui valore assoluto è inferiore a una soglia λ. Per trovare il valore ottimale, esploriamo un range di soglie e misuriamo l'impatto su accuratezza e sparsità:
thresholds = np.linspace(0, 0.1, 11) # 11 valori da 0.0 a 0.1
results = []
total_params = np.sum([param.numel() for name, param in net.named_parameters()
if 'weight' in name])
for threshold in tqdm(thresholds):
# Applica zero pruning: azzera pesi sotto soglia
for name, param in net.named_parameters():
if 'weight' in name:
param.data[torch.abs(param.data) < threshold] = 0
# Conta parametri azzerati
zero_params = np.sum([torch.sum(param == 0).item()
for name, param in net.named_parameters()
if 'weight' in name])
accuracy = evaluate(net)
results.append([threshold, accuracy, total_params, zero_params])
results_df = pd.DataFrame(results,
columns=["Threshold", "Accuracy", "Original Params", "Zero Params"])
results_df["Zero percentage"] = 100 * results_df["Zero Params"] / results_df["Original Params"]
I risultati mostrano chiaramente il trade-off tra compressione e accuratezza:
| Threshold | Accuracy | Original Params | Zero Params | Zero percentage |
|---|---|---|---|---|
| 0.00 | 96.34% | 566,528 | 0 | 0.00% |
| 0.01 | 96.28% | 566,528 | 120,371 | 21.25% |
| 0.02 | 96.53% | 566,528 | 238,157 | 42.04% |
| 0.03 | 96.73% | 566,528 | 346,546 | 61.17% |
| 0.04 | 94.79% | 566,528 | 422,962 | 74.66% |
| 0.05 | 88.04% | 566,528 | 465,203 | 82.11% |
| 0.06 | 84.00% | 566,528 | 488,371 | 86.20% |
| 0.07 | 82.91% | 566,528 | 504,699 | 89.09% |
| 0.08 | 81.99% | 566,528 | 517,321 | 91.31% |
| 0.09 | 74.04% | 566,528 | 527,215 | 93.06% |
| 0.10 | 67.62% | 566,528 | 534,929 | 94.42% |
La tabella rivela un punto ottimale intorno alla soglia 0.03: eliminiamo il 61% dei parametri con un miglioramento dell'accuratezza (da 96.34% a 96.73%). Questo fenomeno di miglioramento è dovuto alla regolarizzazione implicita del pruning, che riduce l'overfitting.
Selezione della Soglia Ottimale e Conversione Sparse
Basandoci sui risultati, selezioniamo threshold=0.03 e convertiamo il modello in formato sparse per ottenere reali benefici in memoria:
threshold = 0.03
net = torch.load('net.pt')
# Applica pruning con soglia ottimale
for name, param in net.named_parameters():
if 'weight' in name:
param.data[torch.abs(param.data) < threshold] = 0
Rappresentazione come Matrice Sparse
import scipy.sparse as sp
sparse_weights = []
# Conversione a formato CSR (Compressed Sparse Row)
for name, param in net.named_parameters():
if 'weight' in name:
np_weight = param.data.cpu().numpy()
sparse_weights.append(sp.csr_matrix(np_weight))
Dimensione prima del pruning:
total_size = 0
for name, param in net.named_parameters():
if 'weight' in name:
tensor = param.data
total_size += tensor.element_size() * tensor.numel()
tensor_size_mb = total_size / (1024**2)
print(f"Dimensione prima del pruning: {tensor_size_mb:.2f} MB")
# Output: 2.16 MB
Dimensione dopo il pruning (formato sparse):
total_size = 0
for w in sparse_weights:
total_size += w.data.nbytes
csr_size_mb = total_size / (1024**2)
print(f"Dimensione dopo il pruning: {csr_size_mb:.2f} MB")
# Output: 0.84 MB
La compressione ottenuta è notevole: da 2.16 MB a 0.84 MB, una riduzione del 61% che corrisponde esattamente alla percentuale di parametri eliminati. Questo dimostra l'efficacia della rappresentazione sparse nel tradurre la sparsità logica in risparmio di memoria reale.
Low-Rank Factorization
La fattorizzazione a basso rango sfrutta il principio che molte matrici di pesi nelle reti neurali hanno un rango effettivo molto inferiore alle loro dimensioni nominali. Decomponendo una matrice W (m×n) in un prodotto di matrici più piccole, possiamo ridurre drasticamente il numero di parametri.
Setup e Architettura
Utilizziamo lo stesso modello SimpleNet con quattro layer fully connected:
class SimpleNet(nn.Module):
def __init__(self):
super(SimpleNet, self).__init__()
self.fc1 = nn.Linear(28 * 28, 512)
self.fc2 = nn.Linear(512, 256)
self.fc3 = nn.Linear(256, 128)
self.fc4 = nn.Linear(128, 10)
def forward(self, x):
x = x.view(x.size(0), -1)
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
x = torch.relu(self.fc3(x))
x = self.fc4(x)
return x
net = SimpleNet()
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(net.parameters(), lr=0.001)
for epoch in range(5):
net.train()
running_loss = 0.0
for data in trainloader:
inputs, labels = data
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
running_loss += loss.item()
accuracy = evaluate(net)
print(f"Epoch {epoch + 1}, Loss: {running_loss / len(trainloader)}, "
f"Accuracy: {accuracy * 100:.2f}%")
Funzione per il Calcolo delle Operazioni Minime
La moltiplicazione di matrici a catena può essere eseguita in ordini diversi, producendo costi computazionali differenti. Questa funzione ricorsiva calcola il numero minimo di operazioni:
def MatrixChainOrder(p, i, j):
"""
Calcola il numero minimo di moltiplicazioni scalari necessarie
per moltiplicare una catena di matrici.
p: lista delle dimensioni [d0, d1, ..., dn] dove la matrice i ha dimensioni p[i-1] x p[i]
i, j: indici della sottosequenza da considerare
"""
if i == j:
return 0
_min = sys.maxsize
# Prova tutte le possibili parentesizzazioni
for k in range(i, j):
count = (MatrixChainOrder(p, i, k) +
MatrixChainOrder(p, k + 1, j) +
p[i-1] * p[k] * p[j])
if count < _min:
_min = count
return _min
Applicazione della Fattorizzazione attraverso Diversi Rank
Applichiamo la SVD (Singular Value Decomposition) al terzo layer (fc3) con dimensioni 128×256, esplorando diversi valori di rank:
rank_values = [128, 100, 90, 80, 60, 50, 40, 30, 20, 10, 5, 2, 1]
results = []
original_total_params = 128 * 256 # 32,768 parametri originali
batch_size = 32
# Decomposizione SVD del layer fc3
# W = U × S × V^T dove U (128×128), S (128×256 diagonale), V (256×256)
U, S, V = torch.svd(net.fc3.weight)
for rank in tqdm(rank_values):
# Troncamento alle prime 'rank' componenti singolari
U_low_rank = U[:, :rank] # 128 × rank
S_low_rank = torch.diag(S[:rank]) # rank × rank
V_low_rank = V[:, :rank] # 256 × rank
# Ricostruzione: W ≈ U_r × S_r × V_r^T
factorized_weight_matrix = torch.mm(U_low_rank,
torch.mm(S_low_rank, V_low_rank.t()))
# Sostituzione dei pesi del layer
net.fc3.weight = nn.Parameter(factorized_weight_matrix)
# Calcolo operazioni per: [batch_size] × [256×rank] × [rank×rank] × [rank×128]
weight_list = [batch_size, 256, rank, rank, 128]
if rank == 128:
# Matrice completa: nessuna fattorizzazione
total_operations = batch_size * 256 * 128
else:
# Trova l'ordine ottimale di moltiplicazione
total_operations = MatrixChainOrder(weight_list, 1, 4)
# Valutazione con 7 run per stabilità statistica
accuracies = 0
total_time = 0
for _ in range(7):
start = time()
accuracies += evaluate(net)
total_time += time() - start
# Parametri totali: U (128×rank) + S (rank×rank) + V (256×rank)
new_total_params = 128*rank + rank**2 + rank*256
results.append([rank, 100*accuracies/7, original_total_params,
new_total_params, total_operations, total_time/7])
results_df = pd.DataFrame(results,
columns=["Rank", "Accuracy", "Original Params",
"New Params", "Operations", "Inference Time"])
I risultati mostrano il trade-off tra riduzione dei parametri e mantenimento dell'accuratezza:
| Rank | Accuracy | Original Params | New Params | Operations | Inference Time |
|---|---|---|---|---|---|
| 128 | 97.24% | 32,768 | 65,536 | 1,048,576 | 1.27s |
| 100 | 97.24% | 32,768 | 48,400 | 1,548,800 | 1.35s |
| 90 | 97.26% | 32,768 | 42,660 | 1,365,120 | 1.41s |
| 80 | 97.26% | 32,768 | 37,120 | 1,187,840 | 1.44s |
| 60 | 97.26% | 32,768 | 26,640 | 852,480 | 1.41s |
| 50 | 97.23% | 32,768 | 21,700 | 694,400 | 1.43s |
| 40 | 97.25% | 32,768 | 16,960 | 542,720 | 1.50s |
| 30 | 97.23% | 32,768 | 12,420 | 397,440 | 1.54s |
| 20 | 97.16% | 32,768 | 8,080 | 258,560 | 1.57s |
| 10 | 97.24% | 32,768 | 3,940 | 126,080 | 1.52s |
| 5 | 80.23% | 32,768 | 1,945 | 62,240 | 1.82s |
| 2 | 34.73% | 32,768 | 772 | 24,704 | 1.59s |
| 1 | 19.08% | 32,768 | 385 | 12,320 | 1.58s |
La tabella rivela pattern interessanti:
- Rank 60-100: Accuratezza praticamente identica al modello originale (~97.25%) con riduzione dei parametri del 18-48%
- Rank 20-40: Perdita minima di accuratezza (<0.1%) con riduzione del 62-75%
- Rank 10: Ancora 97.24% di accuratezza con solo 3,940 parametri (riduzione dell'88%)
- Rank <10: Crollo drastico dell'accuratezza, indicando che il rango intrinseco della matrice è intorno a 10
Un aspetto controintuitivo è l'aumento dei parametri per rank=128 (da 32,768 a 65,536). Questo accade perché stiamo memorizzando tre matrici separate invece di una sola, senza alcun beneficio di compressione.
Quantization
La quantizzazione è la tecnica più immediata da implementare e offre benefici garantiti in termini di riduzione della memoria. Converte i pesi da rappresentazioni in virgola mobile a precisione piena (float32, 4 bytes) a rappresentazioni a precisione ridotta (int8, 1 byte).
Quantizzazione Dinamica Post-Training
PyTorch offre utility integrate che rendono la quantizzazione estremamente semplice:
# Quantizzazione del modello addestrato a int8
quantized_model = torch.quantization.quantize_dynamic(
net, # Modello originale
{torch.nn.Linear}, # Tipi di layer da quantizzare
dtype=torch.qint8 # Tipo di dato target (int8)
)
# Valutazione immediata senza riaddestramento
quantized_accuracy = evaluate(quantized_model)
print(f"Quantized Model Accuracy: {quantized_accuracy * 100:.2f}%")
# Output: 97.24%
Vantaggi della Quantizzazione
La quantizzazione dinamica post-training offre diversi vantaggi:
- Semplicità: Una singola chiamata di funzione, nessun riaddestramento necessario
- Riduzione garantita: 4x riduzione teorica della dimensione (float32 → int8)
- Accuratezza preservata: Nel nostro caso, 97.24% identico al modello originale
- Accelerazione hardware: Su processori con supporto int8, le operazioni sono significativamente più veloci
La quantizzazione è particolarmente efficace quando combinata con altre tecniche. Ad esempio, applicando prima il pruning e poi la quantizzazione sui pesi rimanenti, si possono ottenere fattori di compressione superiori a 35x mantenendo accuratezza accettabile.
Confronto e considerazioni Finali
Ogni tecnica offre caratteristiche e trade-off specifici che la rendono più o meno adatta a scenari diversi:
Knowledge Distillation
- Riduzione dell'accuratezza: ~2.5% (da 98.79% a 96.33%)
- Accelerazione: ~14% più veloce
- Ideale per: Trasferire conoscenza da ensemble o modelli molto grandi a architetture deployment-friendly
Pruning (soglia 0.03)
- Riduzione parametri: 61%
- Riduzione memoria: 61% (2.16 MB → 0.84 MB)
- Accuratezza: 96.73% (miglioramento rispetto all'originale)
- Ideale per: Modelli fully connected, deployment su dispositivi con memoria limitata
Low-Rank Factorization (rank 60)
- Riduzione parametri: 18.7% (32,768 → 26,640 per il layer fc3)
- Accuratezza: 97.26% (praticamente identica)
- Ideale per: Layer densi specifici, controllo granulare della compressione
Quantization
- Riduzione memoria: 4x teorica (float32 → int8)
- Accuratezza: 97.24% (preservata completamente)
- Ideale per: Implementazione rapida, deployment su hardware con accelerazione int8
La scelta della tecnica dipende dai vincoli specifici dell'applicazione: latenza target, memoria disponibile, accuratezza minima richiesta e capacità hardware. In scenari reali, la combinazione di più tecniche (ad esempio pruning + quantization) può sbloccare fattori di compressione molto superiori a quelli ottenibili con approcci singoli.







Commenti dalla community