Tabella dei Contenuti
L’analisi delle reti (network analysis) è una metodologia utilizzata per rappresentare e studiare sistemi composti da elementi connessi tra loro. Le reti permettono di modellare e interpretare fenomeni complessi osservando non solo le singole entità, ma anche e soprattutto le relazioni che le legano.
In molte situazioni, infatti, non è tanto il comportamento dei singoli nodi a determinare la struttura di un sistema, quanto il modo in cui questi nodi interagiscono. Questo approccio si rivela utile in contesti molto diversi tra loro, dalla biologia alle scienze sociali, dall’epidemiologia alla linguistica computazionale, dall’analisi delle infrastrutture alla comprensione di narrazioni letterarie.
Ragionare in termini di rete consente di spostare il focus dall’analisi individuale all’analisi relazionale. È possibile identificare elementi centrali, gruppi coesi, connessioni deboli o ridondanti, strutture gerarchiche o distribuite. Inoltre, le metriche topologiche offerte dalla teoria dei grafi permettono di misurare concetti come influenza, intermediazione, prossimità e isolamento, fornendo un supporto quantitativo a interpretazioni altrimenti intuitive.
L’obiettivo di questo articolo è mostrare come queste tecniche possano essere applicate anche a un corpus letterario. Attraverso la libreria Python chiamata NetworkX, utilizzeremo il grafo dei personaggi di Les Misérables per esplorare passo dopo passo la costruzione di una rete, la sua pulizia, la sua analisi strutturale e la sua visualizzazione. L’interesse principale non sarà quello di costruire un modello predittivo, ma piuttosto di isolare pattern strutturali significativi, capire cosa rende alcuni personaggi più “centrali” di altri, quali gruppi narrativi emergono spontaneamente, e come le dinamiche del racconto si riflettano nella topologia della rete.
Nel corso dell’analisi, verrà data particolare attenzione al problema del rumore informativo: nelle reti letterarie, infatti, molte co-occorrenze tra personaggi possono essere marginali o casuali. Così come nella gestione dei dati mancanti è necessario distinguere tra assenze casuali e sistematiche, anche in una rete è fondamentale saper filtrare le connessioni deboli per evitare distorsioni nella struttura. Il concetto di “pulizia del grafo” sarà quindi centrale per garantire che l’analisi successiva restituisca segnali affidabili e interpretabili.
La struttura dell’articolo seguirà un percorso ordinato: si partirà dal caricamento del grafo grezzo, si procederà con un filtraggio delle connessioni meno significative, si calcoleranno le principali metriche strutturali e si esploreranno le comunità latenti presenti nel testo. Infine, si proporranno visualizzazioni efficaci per restituire in forma grafica i risultati ottenuti.
L’approccio sarà incrementale e riproducibile, con esempi di codice Python ad ogni passaggio. L’analisi sarà accompagnata da visualizzazioni statiche (con matplotlib) e interattive (con pyvis), utili sia per l’analisi esplorativa sia per la presentazione dei risultati.
- Come costruire, pulire e analizzare una rete di personaggi letterari usando NetworkX
- A riconoscere pattern strutturali e comunità latenti all’interno di un testo narrativo
- A creare visualizzazioni statiche e interattive per raccontare i risultati in modo chiaro ed efficace
Cosa è una rete: struttura e formulazione
Una rete (o grafo) è una rappresentazione matematica di un sistema composto da elementi (nodi) connessi tra loro tramite relazioni (archi). Formalmente, una rete si definisce come un grafo \( G = (V, E) \), dove \( \text{V} \) è l’insieme dei nodi (o vertici) e \( E \subseteq V \times V \) è l’insieme degli archi (o lati). Se gli archi hanno una direzione, si parla di grafo orientato; altrimenti, il grafo è detto non orientato. Se gli archi hanno un peso associato, ad esempio la frequenza di interazione, si parla di grafo pesato.
Nel nostro caso, studieremo un grafo non orientato e pesato in cui:
- ogni nodo rappresenta un personaggio,
- ogni arco collega due personaggi che compaiono insieme in almeno una scena o capitolo,
- il peso dell’arco corrisponde al numero di co-occorrenze.
I grafi possono essere rappresentati in diversi modi:
- come liste di adiacenza, dove per ogni nodo si elencano i suoi vicini;
- come matrici di adiacenza, ovvero matrici quadrate in cui l’elemento \( A_{i,j} \) indica la presenza (e nel caso pesato, l’intensità) di un collegamento tra i nodi \( \text{i} \) e \( \text{j} \);
- come liste di archi, cioè coppie (o terne se il grafo è pesato) che indicano le connessioni.
Una proprietà fondamentale di un nodo è il grado: nel caso di un grafo non orientato, il grado \( d(v) \) di un nodo \( \text{v} \) è il numero di archi incidenti su di esso. Nei grafi pesati, si parla anche di grado pesato, cioè la somma dei pesi degli archi incidenti. Nei grafi orientati, si distingue tra grado entrante (numero di archi che arrivano) e grado uscente (numero di archi che partono).
Un altro concetto chiave è la componente connessa: un sottografo in cui tutti i nodi sono collegati tra loro tramite percorsi, e che non può essere esteso con altri nodi del grafo mantenendo questa proprietà. Nei grafi non connessi esistono più componenti, e spesso solo la componente principale è oggetto di analisi.
La distanza tra due nodi è il numero minimo di archi che bisogna attraversare per andare dall’uno all’altro. Su questa base si definiscono proprietà globali come:
- diametro del grafo: la massima distanza tra due nodi qualunque;
- path length medio: la media delle distanze tra tutte le coppie di nodi.
Altre metriche importanti sono:
- il coefficiente di clustering, che misura la tendenza dei vicini di un nodo a essere a loro volta connessi;
- la centralità, che assume varie forme (degree, betweenness, closeness, eigenvector) e quantifica l’importanza o l’influenza di un nodo nella rete.
I grafi possono essere sparsi o densi, a seconda della proporzione di archi presenti rispetto al numero massimo possibile \( \frac{n(n - 1)}{2} \) per un grafo non orientato con \( \text{n} \) nodi). La densità è quindi definita come:
\[ \text{Densità} = \frac{2|E|}{|V|(|V| - 1)} \]
Infine, un grafo può essere statico o dinamico: nel nostro caso analizziamo un grafo statico, cioè costruito a partire dall’intera narrazione e non variabile nel tempo. Tuttavia, l’analisi dinamica delle reti, in cui i nodi e gli archi cambiano nel tempo, è un campo in forte espansione, particolarmente rilevante in ambiti come l’epidemiologia o l’analisi dei social network.
Caricamento del grafo
Per analizzare una rete, devi prima costruirla. In questa sezione useremo un dataset classico nella letteratura della network science: la rete dei personaggi de I Miserabili di Victor Hugo. È un caso esemplare di come si possano modellare dati narrativi in forma di grafo, con personaggi come nodi e co-occorrenze come archi.
Dataset: les_miserables_graph()
Questo grafo è disponibile direttamente tramite la libreria networkx, che fornisce un set di dati precostruiti per scopi educativi. È un grafo ponderato, non orientato.

- Nodi: personaggi del romanzo
- Archi: connessioni tra personaggi che appaiono nella stessa scena o sezione narrativa
- Peso: rappresenta la frequenza della co-occorrenza (più alto = più interazioni)
Questa rete permette di studiare in modo quantitativo la struttura narrativa e il ruolo relativo dei personaggi nella storia.
Caricamento e statistiche iniziali
import networkx as nx
import matplotlib.pyplot as plt
# Caricamento del grafo dei Miserabili
G = nx.les_miserables_graph()
# Numero di nodi e archi
n_nodi = G.number_of_nodes()
n_archi = G.number_of_edges()
# Densità della rete
densità = nx.density(G)
print(f"Numero di nodi: {n_nodi}")
print(f"Numero di archi: {n_archi}")
print(f"Densità: {densità:.4f}")
>>>
Numero di nodi: 77
Numero di archi: 254
Densità: 0.0868Interpretazione
- Numero di nodi: rappresenta il numero totale di personaggi.
- Numero di archi: indica quante coppie di personaggi sono collegate almeno una volta.
- Densità: misura quanto la rete è connessa rispetto al massimo teorico (valori vicini a 1 = rete densa; vicini a 0 = rete sparsa).
Istogramma dei pesi degli archi
I pesi sono fondamentali per distinguere legami forti da quelli deboli. Molti archi appaiono solo una o due volte; pochi appaiono frequentemente.
import seaborn as sns
# Estrazione dei pesi
pesi = [d['weight'] for u, v, d in G.edges(data=True)]
# Istogramma dei pesi
plt.figure(figsize=(8, 5))
sns.histplot(pesi, bins=range(1, max(pesi)+2), kde=False)
plt.xlabel("Peso degli archi (frequenza co-occorrenze)")
plt.ylabel("Numero di archi")
plt.title("Distribuzione dei pesi nella rete di Les Misérables")
plt.tight_layout()
plt.show()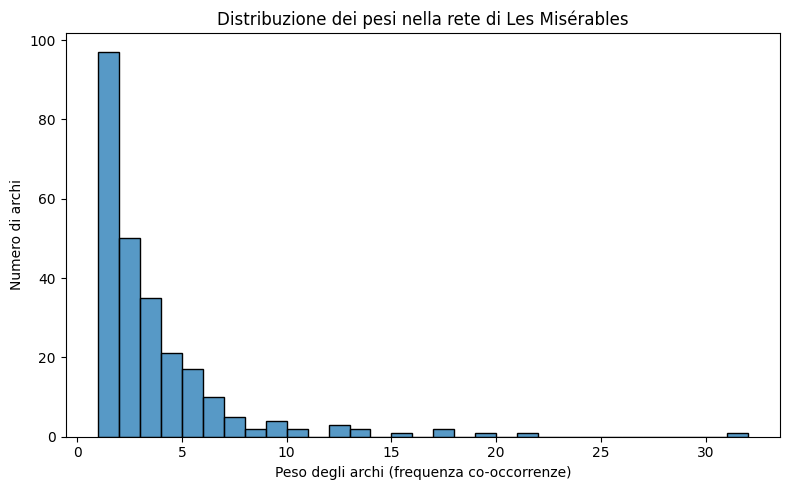
Osservazioni
- L’istogramma mostra una distribuzione right-skewed: la maggior parte delle co-occorrenze è rara.
- Questo è tipico nei network reali, dove pochi nodi o connessioni sono molto attivi, e molti sono marginali.
- Questa informazione sarà utile nella sezione di pulizia, dove rimuoveremo legami deboli.
Rappresentazione iniziale della rete
Per avere un’idea visiva della rete, possiamo disegnarla tutta:
plt.figure(figsize=(10, 10))
pos = nx.spring_layout(G, seed=42)
nx.draw_networkx_nodes(G, pos, node_size=50)
nx.draw_networkx_edges(G, pos, alpha=0.3)
nx.draw_networkx_labels(G, pos, font_size=8)
plt.title("Rete completa dei personaggi di Les Misérables")
plt.axis('off')
plt.show()
Questa rappresentazione mostra:
- La struttura complessiva del grafo
- La presenza di personaggi centrali (posizionati al centro dal layout)
- La densità e la complessità delle interconnessioni
Considerazioni preliminari
- La rete è non orientata: il legame tra A e B implica anche il legame tra B e A.
- Il grafo è ponderato: questo permetterà di distinguere relazioni più o meno significative.
- Non è filtrata: tutti i legami, anche quelli deboli (una sola co-occorrenza), sono presenti.
Questa configurazione iniziale ci permette di procedere con le fasi successive: pulizia, analisi strutturale, rilevamento delle comunità, e visualizzazione mirata.
Python for Social Network Analysis
Impara ad analizzare reti sociali con Python, usando librerie come NetworkX. Un corso della University of Michigan che unisce teoria dei grafi, visualizzazione, e data science applicata. Ottimo per sociologi, analisti e data scientist.
Pulizia e isolamento del segnale
Il grafo iniziale dei personaggi di Les Misérables contiene ogni co-occorrenza tra personaggi nel testo. Questo include anche legami molto deboli: personaggi che si incrociano solo una volta o in contesti marginali. Tali connessioni introducono rumore e possono distorcere l’analisi strutturale e la visualizzazione. Per avere un quadro migliore è opportuno isolare i legami narrativi più significativi eliminando quelli che appaiono troppo raramente. Il risultato è un grafo più semplice, più leggibile e strutturalmente più informativo.
Strategie di pulizia
Useremo un approccio in tre fasi:
- Rimozione degli archi con peso inferiore a una soglia
→ Escludiamo le relazioni che compaiono meno di X volte (es. < 3) - Rimozione dei nodi isolati
→ Dopo aver rimosso gli archi deboli, possono restare nodi senza connessioni - Confronto tra rete originale e filtrata
→ Valutiamo come cambia la struttura: numero di componenti, distribuzione dei gradi, dimensione della componente principale
Rimozione degli archi deboli
Molti archi appaiono solo una o due volte. Questo può essere dovuto a comparse fugaci o coincidenze narrative. Impostiamo una soglia di peso minimo per conservare solo le relazioni più frequenti.
# Soglia minima per il peso degli archi
soglia_peso = 3
# Creazione di una copia del grafo filtrato
G_filtrato = nx.Graph()
for u, v, d in G.edges(data=True):
if d['weight'] >= soglia_peso:
G_filtrato.add_edge(u, v, weight=d['weight'])
# Aggiunta dei nodi connessi
G_filtrato.add_nodes_from(G.nodes(data=True))
print(f"Numero di nodi prima del filtro: {G.number_of_nodes()}")
print(f"Numero di archi prima del filtro: {G.number_of_edges()}")
print(f"Numero di nodi dopo il filtro: {G_filtrato.number_of_nodes()}")
print(f"Numero di archi dopo il filtro: {G_filtrato.number_of_edges()}")
>>>
Numero di nodi prima del filtro: 77
Numero di archi prima del filtro: 254
Numero di nodi dopo il filtro: 77
Numero di archi dopo il filtro: 107Rimozione dei nodi isolati
Dopo aver rimosso gli archi deboli, alcuni nodi rimangono senza connessioni. Questi personaggi non interagiscono più con nessuno nella rete filtrata: vanno rimossi per mantenere coerenza.
# Rimozione dei nodi isolati
nodi_isolati = list(nx.isolates(G_filtrato))
G_filtrato.remove_nodes_from(nodi_isolati)
print(f"Nodi isolati rimossi: {len(nodi_isolati)}")
print(f"Numero finale di nodi: {G_filtrato.number_of_nodes()}")
>>>
Nodi isolati rimossi: 33
Numero finale di nodi: 44Confronto strutturale: rete originale vs filtrata
Ora possiamo confrontare alcune metriche strutturali tra il grafo originale e quello pulito.
Numero di componenti connesse
Una componente è un sottoinsieme di nodi connessi tra loro. Una rete coesa ha poche componenti grandi.
componenti_orig = nx.number_connected_components(G)
componenti_filt = nx.number_connected_components(G_filtrato)
print(f"Componenti nella rete originale: {componenti_orig}")
print(f"Componenti nella rete filtrata: {componenti_filt}")
>>>
Componenti nella rete originale: 1
Componenti nella rete filtrata: 3Distribuzione dei gradi
Il grado di un nodo è il numero di connessioni. Confrontiamo la distribuzione dei gradi prima e dopo il filtro.
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
gradi_orig = [d for n, d in G.degree()]
gradi_filt = [d for n, d in G_filtrato.degree()]
# Istogrammi comparativi
df_gradi = pd.DataFrame({
'Grado': gradi_orig + gradi_filt,
'Tipo': ['Originale']*len(gradi_orig) + ['Filtrata']*len(gradi_filt)
})
plt.figure(figsize=(8, 5))
sns.histplot(data=df_gradi, x='Grado', hue='Tipo', element='step', common_norm=False)
plt.title("Distribuzione dei gradi: Originale vs Filtrata")
plt.tight_layout()
plt.show()
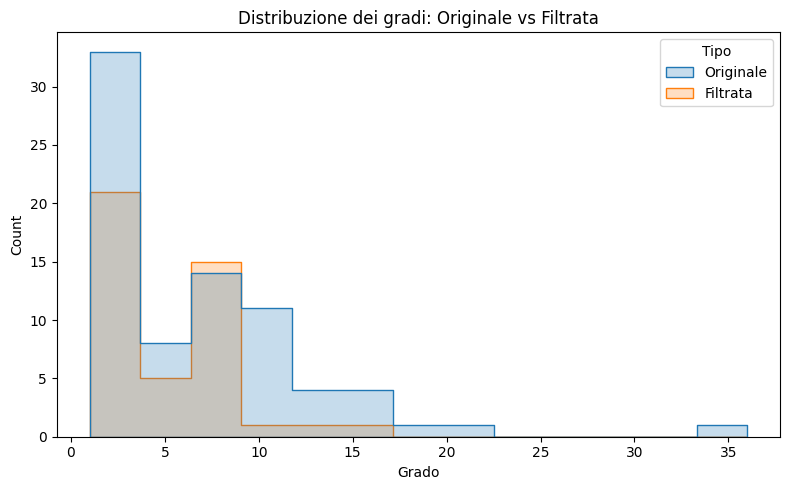
Osservazioni:
- La rete filtrata ha meno nodi con grado basso.
- I personaggi marginali (grado 1–2) vengono eliminati.
- I nodi ad alto grado restano: sono i personaggi centrali della storia.
Dimensione della componente principale
Spesso la componente connessa più grande rappresenta il “cuore” narrativo della rete.
comp_orig = max(nx.connected_components(G), key=len)
comp_filt = max(nx.connected_components(G_filtrato), key=len)
print(f"Nodi nella componente principale (originale): {len(comp_orig)}")
print(f"Nodi nella componente principale (filtrata): {len(comp_filt)}")
>>>
Nodi nella componente principale (originale): 77
Nodi nella componente principale (filtrata): 40Risultato atteso:
- La componente principale nella rete filtrata è più piccola, ma più densa.
- Le connessioni deboli che univano sottogruppi marginali sono state rimosse.
Perché filtrare?
Motivi pratici:
- Riduzione del rumore: i legami occasionali distorcono l’analisi della centralità.
- Visualizzazione migliore: meno nodi = meno caos visivo.
- Analisi più interpretabile: i cluster e le comunità diventano più chiari.
Controindicazioni:
- Rischio di rimuovere personaggi “ponte” con pochi ma importanti legami.
- Perdita di contesto narrativo secondario (comparse episodiche).
Raccomandazioni
- Non esiste una soglia “giusta” universale: dipende dall’obiettivo dell’analisi.
- È utile testare più soglie e confrontare l’impatto sulla struttura.
- Per alcuni scopi (es. analisi della trama completa), può essere utile lavorare anche sulla rete originale non filtrata.
Analisi strutturale
Una volta pulita la rete, possiamo iniziare a indagarne la struttura. Le metriche strutturali aiutano a capire come si organizzano le relazioni tra i nodi, quali elementi sono centrali e come si distribuiscono i legami. In un contesto narrativo, questo significa: chi sono i protagonisti, quali personaggi fanno da ponte tra sottotrame, e se esistono gruppi coesi di personaggi che interagiscono più spesso tra loro.
Distribuzione dei gradi
Il grado di un nodo è il numero di connessioni (archi) che possiede. In una rete narrativa, i nodi ad alto grado sono personaggi che interagiscono con molti altri.
gradi = dict(G_filtrato.degree())
df_gradi = pd.DataFrame({'Personaggio': list(gradi.keys()), 'Grado': list(gradi.values())})
df_gradi = df_gradi.sort_values(by='Grado', ascending=False)
print("Top 10 personaggi per numero di connessioni:")
print(df_gradi.head(10))
>>>
Top 10 personaggi per numero di connessioni:
Personaggio Grado
3 Valjean 15
15 Enjolras 12
14 Marius 10
4 Fantine 9
34 Bossuet 9
32 Courfeyrac 9
6 Thenardier 8
31 Combeferre 8
22 Zephine 7
21 Dahlia 7Visualizzazione:
import seaborn as sns
import matplotlib.pyplot as plt
plt.figure(figsize=(8, 5))
sns.histplot(df_gradi['Grado'], bins=range(1, max(df_gradi['Grado'])+1))
plt.xlabel("Grado")
plt.ylabel("Numero di personaggi")
plt.title("Distribuzione dei gradi nella rete filtrata")
plt.tight_layout()
plt.show()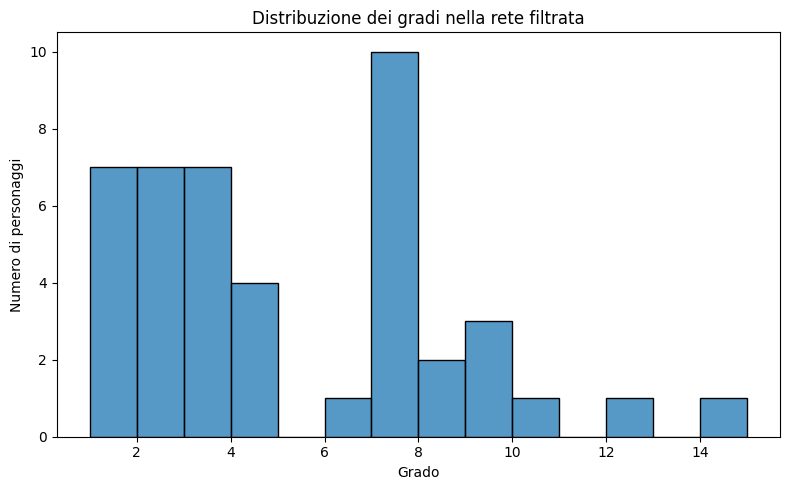
Cosa osservare:
- La distribuzione è tipicamente "long tail": pochi nodi con alto grado, molti con grado basso.
- Questo è coerente con le reti reali e riflette la struttura gerarchica della narrazione.
Centralità
Degree centrality
Misura la centralità in base al numero di connessioni dirette.
centralità_degree = nx.degree_centrality(G_filtrato)
centralità_degree
>>>
{'Myriel': 0.06976744186046512,
'MlleBaptistine': 0.06976744186046512,
'MmeMagloire': 0.06976744186046512,
'Valjean': 0.3488372093023256,
'Fantine': 0.20930232558139533,
'MmeThenardier': 0.06976744186046512,
'Thenardier': 0.18604651162790697,
'Cosette': 0.09302325581395349,
'Javert': 0.09302325581395349,
'Fauchelevent': 0.046511627906976744,
'Simplice': 0.023255813953488372,
'Judge': 0.046511627906976744,
'Champmathieu': 0.046511627906976744,
'Woman2': 0.023255813953488372,
'Marius': 0.23255813953488372,
'Enjolras': 0.27906976744186046,
'Listolier': 0.16279069767441862,
'Tholomyes': 0.16279069767441862,
'Fameuil': 0.16279069767441862,
'Blacheville': 0.16279069767441862,
'Favourite': 0.16279069767441862,
'Dahlia': 0.16279069767441862,
'Zephine': 0.16279069767441862,
'Eponine': 0.046511627906976744,
'Gueulemer': 0.09302325581395349,
'Babet': 0.09302325581395349,
'Claquesous': 0.06976744186046512,
'Brujon': 0.06976744186046512,
'Gillenormand': 0.06976744186046512,
'MotherInnocent': 0.023255813953488372,
'Gavroche': 0.16279069767441862,
'Combeferre': 0.18604651162790697,
'Courfeyrac': 0.20930232558139533,
'Bahorel': 0.16279069767441862,
'Bossuet': 0.20930232558139533,
'Joly': 0.16279069767441862,
'MlleGillenormand': 0.046511627906976744,
'Mabeuf': 0.023255813953488372,
'MotherPlutarch': 0.023255813953488372,
'Prouvaire': 0.046511627906976744,
'Feuilly': 0.13953488372093023,
'Grantaire': 0.046511627906976744,
'Child1': 0.023255813953488372,
'Child2': 0.023255813953488372}Betweenness centrality
Indica quanto un nodo si trovi “in mezzo” a molti cammini: misura l’influenza come ponte tra gruppi.
centralità_betweenness = nx.betweenness_centrality(G_filtrato, normalized=True)
centralità_betweenness
>>>
{'Myriel': 0.06976744186046512,
'MlleBaptistine': 0.06976744186046512,
'MmeMagloire': 0.06976744186046512,
'Valjean': 0.3488372093023256,
'Fantine': 0.20930232558139533,
'MmeThenardier': 0.06976744186046512,
'Thenardier': 0.18604651162790697,
'Cosette': 0.09302325581395349,
'Javert': 0.09302325581395349,
'Fauchelevent': 0.046511627906976744,
'Simplice': 0.023255813953488372,
'Judge': 0.046511627906976744,
'Champmathieu': 0.046511627906976744,
'Woman2': 0.023255813953488372,
'Marius': 0.23255813953488372,
'Enjolras': 0.27906976744186046,
'Listolier': 0.16279069767441862,
'Tholomyes': 0.16279069767441862,
'Fameuil': 0.16279069767441862,
'Blacheville': 0.16279069767441862,
'Favourite': 0.16279069767441862,
'Dahlia': 0.16279069767441862,
'Zephine': 0.16279069767441862,
'Eponine': 0.046511627906976744,
'Gueulemer': 0.09302325581395349,
'Babet': 0.09302325581395349,
'Claquesous': 0.06976744186046512,
'Brujon': 0.06976744186046512,
'Gillenormand': 0.06976744186046512,
'MotherInnocent': 0.023255813953488372,
'Gavroche': 0.16279069767441862,
'Combeferre': 0.18604651162790697,
'Courfeyrac': 0.20930232558139533,
'Bahorel': 0.16279069767441862,
'Bossuet': 0.20930232558139533,
'Joly': 0.16279069767441862,
'MlleGillenormand': 0.046511627906976744,
'Mabeuf': 0.023255813953488372,
'MotherPlutarch': 0.023255813953488372,
'Prouvaire': 0.046511627906976744,
'Feuilly': 0.13953488372093023,
'Grantaire': 0.046511627906976744,
'Child1': 0.023255813953488372,
'Child2': 0.023255813953488372}Eigenvector centrality
Misura quanto un nodo è centrale rispetto ad altri nodi centrali. Tiene conto della qualità delle connessioni.
centralità_eigen = nx.eigenvector_centrality(G_filtrato, max_iter=1000)
centralità_eigen
>>>
{'Myriel': 0.027761470549625144,
'MlleBaptistine': 0.027761470549625144,
'MmeMagloire': 0.027761470549625144,
'Valjean': 0.15420754268270412,
'Fantine': 0.07934468542868024,
'MmeThenardier': 0.03566964034838569,
'Thenardier': 0.04734737288226724,
'Cosette': 0.06792001873160834,
'Javert': 0.0878067090427918,
'Fauchelevent': 0.02077606244832161,
'Simplice': 0.020412042236639855,
'Judge': 0.023526135765722565,
'Champmathieu': 0.023526135765722565,
'Woman2': 0.020412042236639855,
'Marius': 0.2725170202423022,
'Enjolras': 0.3824550913907736,
'Listolier': 0.05105456174519463,
'Tholomyes': 0.05105456174519463,
'Fameuil': 0.05105456174519463,
'Blacheville': 0.05105456174519463,
'Favourite': 0.05105456174519463,
'Dahlia': 0.05105456174519463,
'Zephine': 0.05105456174519463,
'Eponine': 0.042339326950575046,
'Gueulemer': 0.009938473251010329,
'Babet': 0.009938473251010329,
'Claquesous': 0.008898310132608776,
'Brujon': 0.008898310132608776,
'Gillenormand': 0.05072591765336358,
'MotherInnocent': 0.0027500733174009506,
'Gavroche': 0.30077515158153834,
'Combeferre': 0.3317172113517371,
'Courfeyrac': 0.3429410895295125,
'Bahorel': 0.29986172617222245,
'Bossuet': 0.3429410895295125,
'Joly': 0.29986172617222245,
'MlleGillenormand': 0.042786484775632565,
'Mabeuf': 2.0927289158366554e-83,
'MotherPlutarch': 2.0927289158366554e-83,
'Prouvaire': 0.09601798664563198,
'Feuilly': 0.2647030731708414,
'Grantaire': 0.09601798664563198,
'Child1': 2.0927289158366554e-83,
'Child2': 2.0927289158366554e-83}Classifica della Centralità
df_centralità = pd.DataFrame({
'Personaggio': list(G_filtrato.nodes),
'Degree': pd.Series(centralità_degree),
'Betweenness': pd.Series(centralità_betweenness),
'Eigenvector': pd.Series(centralità_eigen)
})
df_centralità = df_centralità.sort_values(by='Eigenvector', ascending=False)
print("Top 10 personaggi per centralità (Eigenvector):")
print(df_centralità[['Personaggio', 'Eigenvector']].head(10))
>>>
Top 10 personaggi per centralità (Eigenvector):
Personaggio Eigenvector
Enjolras Enjolras 0.382455
Bossuet Bossuet 0.342941
Courfeyrac Courfeyrac 0.342941
Combeferre Combeferre 0.331717
Gavroche Gavroche 0.300775
Joly Joly 0.299862
Bahorel Bahorel 0.299862
Marius Marius 0.272517
Feuilly Feuilly 0.264703
Valjean Valjean 0.154208Clustering coefficient
Il coefficiente di clustering misura quanto i vicini di un nodo tendano a essere connessi tra loro. In ambito narrativo, individua gruppi “coesi” dove i personaggi si incontrano spesso in gruppo.
clustering = nx.clustering(G_filtrato)
df_clust = pd.DataFrame({'Personaggio': list(clustering.keys()), 'Clustering': list(clustering.values())})
print("Media del clustering coefficient:", df_clust['Clustering'].mean())
>>>
Media del clustering coefficient: 0.6535632296995932Visualizzazione:
plt.figure(figsize=(8, 5))
sns.histplot(df_clust['Clustering'], bins=10)
plt.title("Distribuzione del clustering coefficient")
plt.xlabel("Clustering")
plt.ylabel("Numero di personaggi")
plt.tight_layout()
plt.show()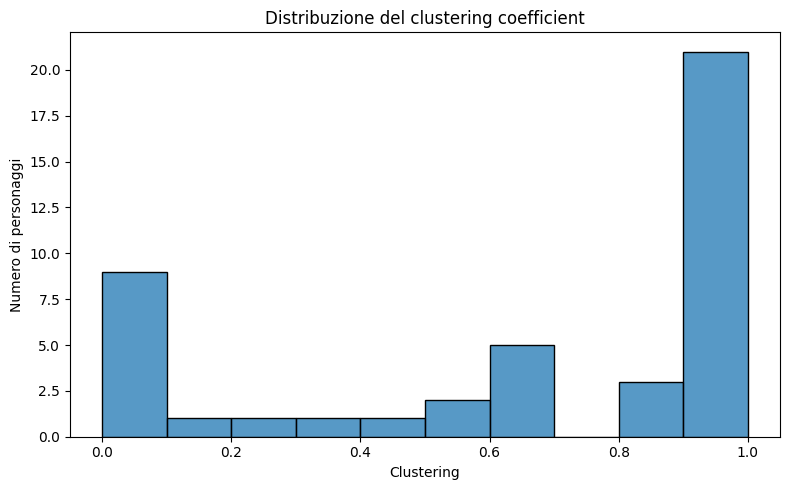
Interpretazione:
- Valori alti indicano sottogruppi narrativi fortemente interconnessi (scene corali).
- Valori bassi suggeriscono ruoli più isolati o di collegamento.
Componenti connesse
Un grafo può avere più componenti (sottografi connessi internamente ma non tra loro). In narrativa, queste componenti rappresentano trame separate o sottotrame poco integrate.
componenti = list(nx.connected_components(G_filtrato))
componenti_ordinate = sorted(componenti, key=len, reverse=True)
print(f"Numero di componenti: {len(componenti)}")
print("Dimensione delle prime 5 componenti:")
for i, comp in enumerate(componenti_ordinate[:5]):
print(f"Componente {i+1}: {len(comp)} nodi")
>>>
Numero di componenti: 3
Dimensione delle prime 5 componenti:
Componente 1: 40 nodi
Componente 2: 2 nodi
Componente 3: 2 nodiVisualizzazione della componente principale
G_principale = G_filtrato.subgraph(componenti_ordinate[0])
plt.figure(figsize=(10, 10))
pos = nx.spring_layout(G_principale, seed=42)
nx.draw_networkx(G_principale, pos, node_size=80, with_labels=True, font_size=8)
plt.title("Componente connessa principale")
plt.axis('off')
plt.show()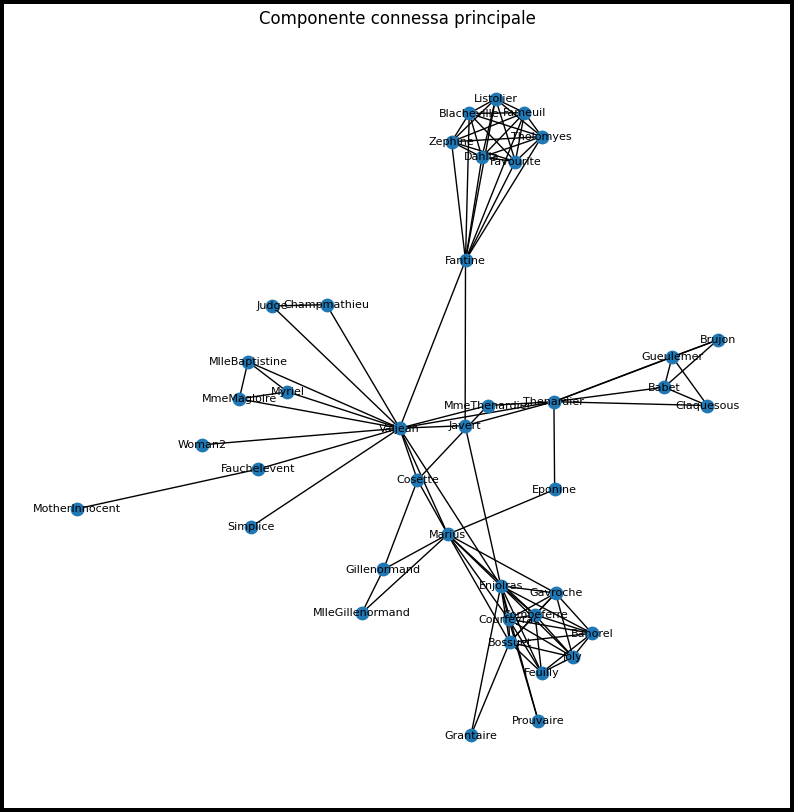
Identificazione delle community
Dopo aver identificato i nodi centrali e le proprietà strutturali della rete, un passo chiave è la rilevazione di comunità: gruppi di nodi che sono più connessi tra loro che con il resto del grafo. In una rete narrativa come quella de I Miserabili, queste comunità possono riflettere sottotrame, ambienti sociali o nuclei familiari.
Algoritmo: Louvain
Il metodo Louvain è uno degli algoritmi di community detection più efficaci e veloci. Ottimizza la modularità, una misura di quanto bene una rete sia divisa in comunità.
Per usarlo in Python serve il pacchetto community (noto anche come python-louvain).
import community as community_louvain
# Calcolo della partizione dei nodi (assegnazione dei cluster)
partizione = community_louvain.best_partition(G_filtrato)
# Aggiungiamo l'informazione di cluster come attributo dei nodi
nx.set_node_attributes(G_filtrato, partizione, 'cluster')Ora ogni nodo ha un attributo cluster che indica il gruppo a cui appartiene.
Statistiche sui cluster
import pandas as pd
df_cluster = pd.DataFrame.from_dict(partizione, orient='index', columns=['Cluster'])
df_cluster['Personaggio'] = df_cluster.index
cluster_counts = df_cluster['Cluster'].value_counts().sort_index()
print("Numero di cluster trovati:", cluster_counts.shape[0])
print("Dimensione dei cluster:")
print(cluster_counts)
>>>
Numero di cluster trovati: 7
Dimensione dei cluster:
Cluster
0 3
1 13
2 8
3 6
4 2
5 10
6 2
Name: count, dtype: int64Visualizzazione dei cluster
Coloriamo i nodi in base al cluster per visualizzare le comunità in modo intuitivo.
import matplotlib.pyplot as plt
import matplotlib.cm as cm
# Mappa di colori
num_cluster = len(set(partizione.values()))
colori = cm.get_cmap('tab20', num_cluster)
# Layout della rete
pos = nx.spring_layout(G_filtrato, seed=42)
# Disegno dei nodi colorati per cluster
plt.figure(figsize=(10, 10))
for cluster_id in range(num_cluster):
nodi_cluster = [n for n in G_filtrato.nodes if partizione[n] == cluster_id]
nx.draw_networkx_nodes(G_filtrato, pos, nodelist=nodi_cluster,
node_size=100,
node_color=[colori(cluster_id)],
label=f"Cluster {cluster_id}")
nx.draw_networkx_edges(G_filtrato, pos, alpha=0.3)
nx.draw_networkx_labels(G_filtrato, pos, font_size=8)
plt.title("Rilevamento delle comunità con Louvain")
plt.legend()
plt.axis('off')
plt.show()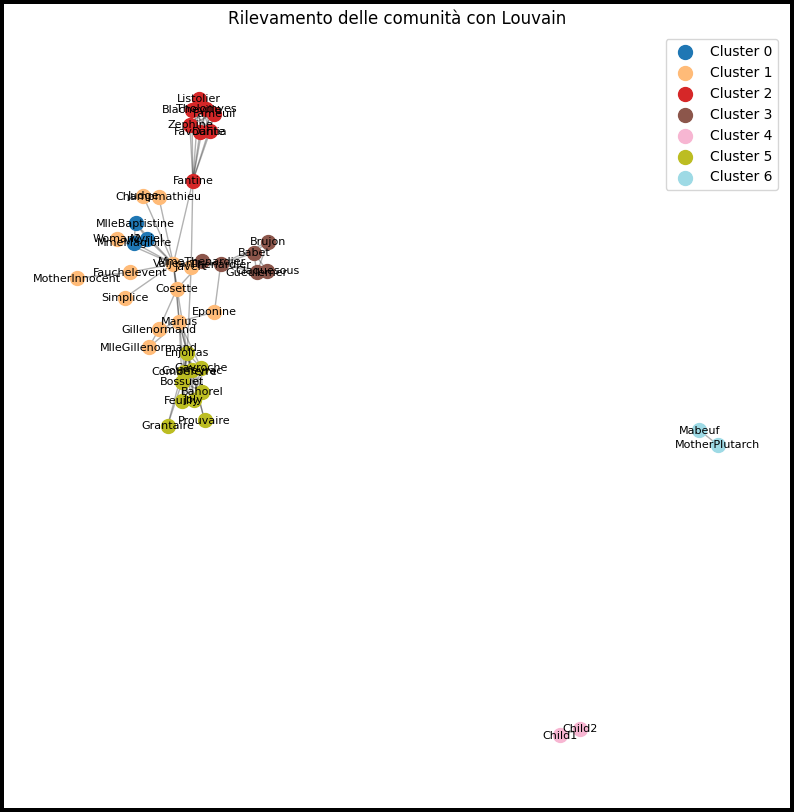
Limiti e considerazioni
Vantaggi del Louvain:
- Efficiente anche su grafi grandi
- Non richiede numero di cluster predefinito
- Ritorna partizioni ben definite
Limiti:
- Il risultato può variare con il layout e la struttura locale
- Non distingue sottocomunità interne ai cluster
- Non è stabile al 100%: esiti leggermente diversi a ogni run
Visualizzazione
Visualizzare una rete complessa come quella di Les Misérables serve a evidenziare pattern nascosti e a rendere l’analisi interpretabile anche da chi non ha familiarità con le metriche formali.
Dimensione dei nodi in base alla centralità
Per enfatizzare i personaggi centrali, possiamo ridimensionare i nodi in base alla eigenvector centrality.
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import networkx as nx
# 1. Estrai la componente connessa più grande
G_comp = G_filtrato.subgraph(max(nx.connected_components(G_filtrato), key=len)).copy()
# 2. Calcola l'eigenvector centrality solo sulla componente
centralità_sub = nx.eigenvector_centrality(G_comp, max_iter=1000, tol=1e-06)
# 3. Inizializza valori a zero per i nodi non nella componente principale
centralità = {n: 0.0 for n in G_filtrato.nodes}
centralità.update(centralità_sub)
# 4. Ottieni l'attributo cluster per colorare
clusters = nx.get_node_attributes(G_filtrato, 'cluster')
num_cluster = len(set(clusters.values()))
cmap = cm.get_cmap('tab20', num_cluster)
# 5. Layout di posizionamento
pos = nx.spring_layout(G_filtrato, seed=42)
# 6. Costruzione dimensioni nodi
dimensioni_nodi = [3000 * centralità[n] for n in G_filtrato.nodes]
# 7. Disegno finale
plt.figure(figsize=(10, 10))
nx.draw_networkx_nodes(G_filtrato, pos,
node_size=dimensioni_nodi,
node_color=[cmap(clusters[n]) for n in G_filtrato.nodes],
alpha=0.8)
nx.draw_networkx_edges(G_filtrato, pos, alpha=0.3)
nx.draw_networkx_labels(G_filtrato, pos, font_size=7)
plt.title("Rete filtrata – dimensione per centralità (eigenvector)")
plt.axis('off')
plt.tight_layout()
plt.show()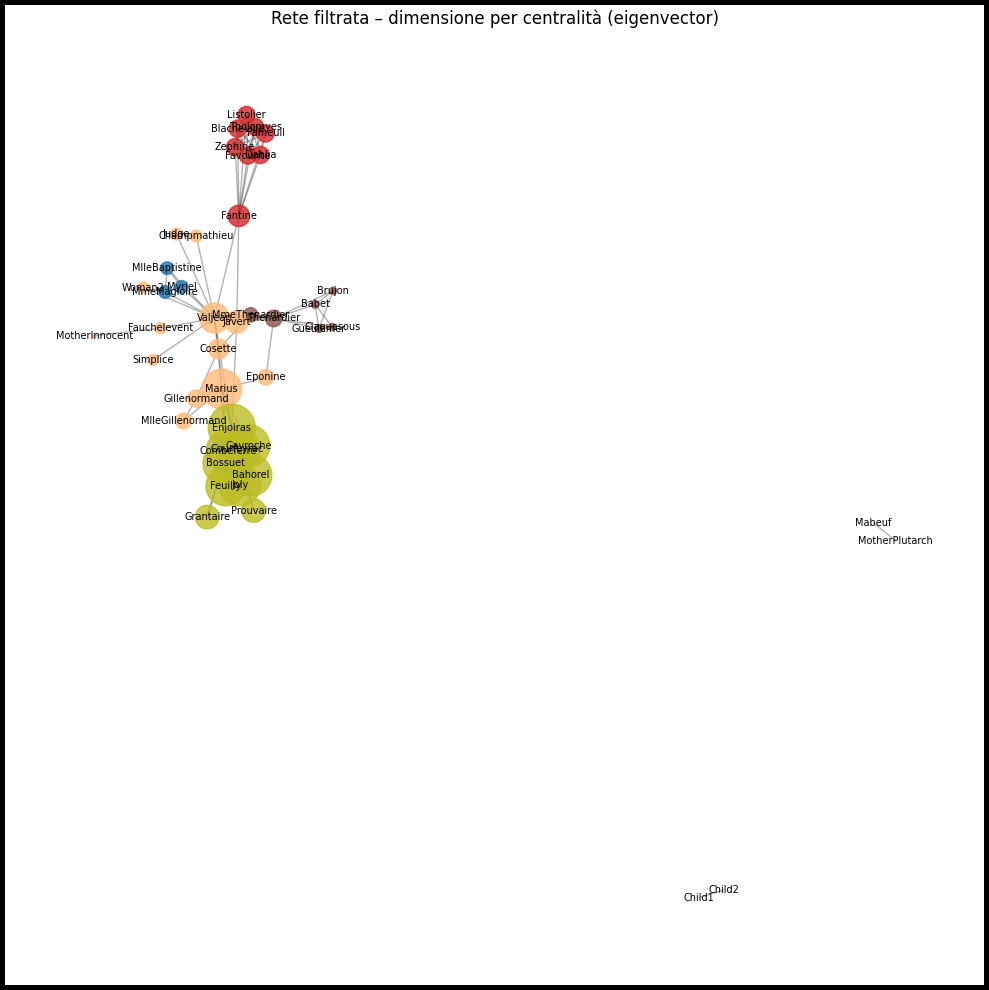
Confronto: rete completa vs rete filtrata
Per capire il valore della pulizia, confrontiamo le due versioni della rete.
# Layout comune per il confronto
pos_all = nx.spring_layout(G, seed=42)
plt.figure(figsize=(15, 6))
# Rete completa
plt.subplot(1, 2, 1)
nx.draw(G, pos_all, node_size=30, edge_color='gray', alpha=0.2)
plt.title("Rete completa (non filtrata)")
plt.axis('off')
# Rete filtrata
plt.subplot(1, 2, 2)
nx.draw(G_filtrato, pos_all, node_size=50, edge_color='gray', alpha=0.5,
node_color=[cmap(clusters[n]) for n in G_filtrato.nodes])
plt.title("Rete filtrata (soglia peso ≥ 3)")
plt.axis('off')
plt.tight_layout()
plt.show()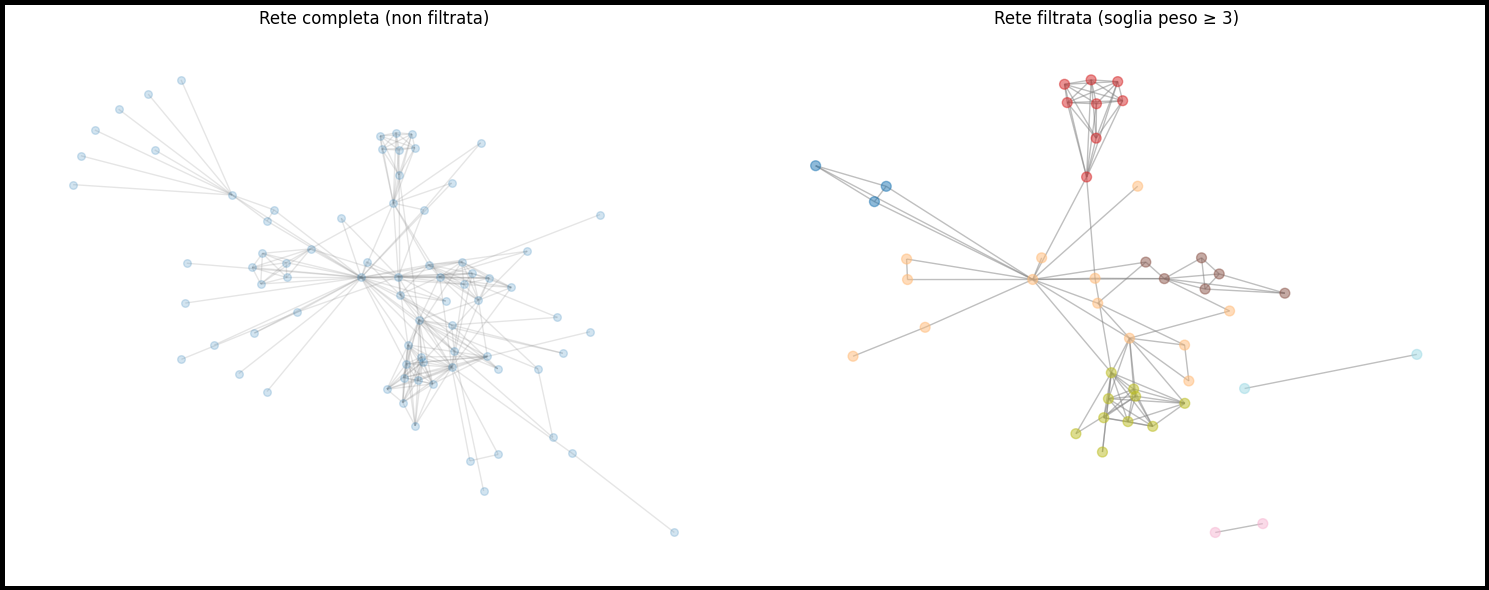
Visualizzazione interattiva con pyvis
Se desideri un'esperienza esplorativa più ricca (hover, zoom, pan), puoi esportare la rete in HTML con pyvis.
from pyvis.network import Network
# Subgrafo visualizzabile (facoltativo: solo componente principale)
G_vis = G_filtrato.subgraph(max(nx.connected_components(G_filtrato), key=len)).copy()
# Crea rete pyvis
net = Network(height='800px', width='100%', notebook=False)
net.from_nx(G_vis)
# Aggiungi cluster e centralità come attributi
for node in net.nodes:
cid = clusters.get(node['id'], 0)
cent = centralità.get(node['id'], 0.0)
node['color'] = f"hsl({cid * 45 % 360}, 80%, 60%)"
node['value'] = cent
# Scrittura HTML (più stabile)
net.write_html("rete_miserables.html", notebook=False, open_browser=True)Considerazioni finali
- L'uso congiunto di colori (per cluster) e dimensioni (per centralità) aumenta la leggibilità.
- I layout fisici come Fruchterman-Reingold distribuiscono bene i nodi, ma l'esito può variare tra esecuzioni.
- La versione interattiva è utile per presentazioni o esplorazioni personali, ma richiede browser e rendering HTML.
Conclusioni
Analizzare reti costruite da dati narrativi, come la rete dei personaggi de I Miserabili, consente di trasformare una storia complessa in una struttura osservabile, misurabile e visualizzabile. L’approccio a grafo permette di:
- identificare i personaggi centrali in modo oggettivo,
- evidenziare sottogruppi coerenti (comunità narrative),
- valutare il ruolo strutturale dei personaggi tramite centralità e clustering.
Cosa si impara da una rete narrativa
- Centralità e ruolo: la rete evidenzia in modo oggettivo quali personaggi sono centrali e quali fungono da collegamento tra scene o sottotrame.
- Comunità e coesione: i cluster identificati corrispondono spesso a gruppi narrativi coerenti, aiutando a comprendere la struttura sociale della storia.
- Pulizia e filtraggio: rimuovere legami deboli migliora la leggibilità e l’informatività della rete, rendendo più visibili le relazioni chiave.
- Visualizzazione: combinare layout, colore e dimensione trasforma un grafo complesso in una mappa utile alla comprensione.
Limiti di questo tipo di rete
- La rete si basa su co-occorrenze, non su relazioni semantiche. Due personaggi che compaiono insieme non necessariamente interagiscono.
- Non c’è direzionalità: le relazioni non distinguono chi agisce e chi riceve.
- Le informazioni temporali sono assenti: la sequenza narrativa è ignorata.
- Non distingue tra tipo o tono delle interazioni (amichevoli, conflittuali, episodiche),
- La rete è sensibile a soglie arbitrarie (es. peso ≥ 3),
La rete non è solo un supporto visivo, ma uno strumento analitico. Filtrare gli archi deboli e rimuovere il rumore migliora significativamente la leggibilità e la qualità dell’analisi.
Queste semplificazioni vanno tenute presenti, soprattutto se si vuole applicare la stessa metodologia ad altri contesti più o meno complessi. Questa analisi fornisce un’introduzione solida all’uso di Python per trattare reti reali, con un'applicazione narrativa che rende immediata l’intuizione dei concetti chiave. Puoi estendere lo stesso approccio ad ambiti completamente diversi: social network, biologia, logistica.







Commenti dalla community