Introduzione alle reti neurali - pesi, bias e attivazione

Questo articolo ha l'obiettivo di comunicarti come funzionano le reti neurali nell'ambito del machine e deep learning.

Le reti neurali sono un particolare tipo di tecnologia che ha completamente rivoluzionato gli ultimi tempi.

Infatti, modelli come GPT e Falcon sono proprio basati su diverse reti neurali che comunicano tra di loro in una architettura particolare chiamata transformer.

Spesso sentiamo dire che le reti neurali artificiali sono delle rappresentazioni dei neuroni cerebrali umani all'interno di un computer.

Questi insiemi di neuroni formano reti interconnesse, ma i loro processi che scatenano eventi e attivazioni sono alquanto diversi da quello di un cervello vero.

Un neurone, preso singolarmente, è relativamente inutile, ma se unito a centinaia o migliaia di altri neuroni formano un rete interconnessa che spesso supera le performance di qualsiasi altro algoritmo di machine learning.

Inizia qui con il Machine Learning e Analisi Dati

Stai iniziando il tuo percorso con Python, Machine Learning e Data Analytics? 👌 Questa pagina ti fornirà il percorso ideale in base al contenuto presente in questo blog. Ogni sezione riporterà gli articoli più idonei per il livello e gli obiettivi del lettore. Ogni sezione sarà inoltre aggiornat…

Diario Di Un Analista | Data Science, Machine Learning & AnalyticsAndrea D’Agostino

Breve background storico

Il concetto di rete neurale è alquanto antico - i primi pensieri di modellare un software prendendo ispirazione dal cervello umano risalgono agli inizi del 1940, da parte di Donald Hebb, McCulloch e Pitts.

Per oltre 20 anni il concetto è rimasto sul piano della teoria, poiché l'addestramento delle reti neurali è stato possibile solo attraverso una maggiore potenza computazione e alla creazione dell'algoritmo di backpropagation da parte di Paul Werbos, un efficiente meccanismo che permette alla rete di imparare propagando il feedback di un neurone a quello che lo precede.

Spicca il lavoro di Geoffrey Hinton, Andrew Ng e Jeff Dean che, insieme ad altri ricercatori, hanno reso il paradigma delle reti neurali popolare e efficace per tutta una serie di problemi.

Oggi le reti neurali vengono utilizzate in una miriade di compiti grazie alla loro abilità di risolvere problemi prima considerati impossibili da risolvere come la traduzione simultanea tra lingue, sintesi di video e audio e guida autonoma.

Differenze tra neurone naturale e artificiale

Anche se è vero che le reti neurali si ispirano ai neuroni naturali, questo paragone è quasi fuorviante poiché le loro anatomie e comportamenti sono diversi.

Non andrò molto nell'aspetto neuroscientifico, ma i neuroni naturali sembrano preferire una attivazione basata su "switch", on oppure off, attività oppure nessuna attività.

In seguito al periodo di attività, tra l'altro, i neuroni naturali mostrano un periodo refrattario, cioè dove la loro abilità di attivarsi nuovamente è soppressa.

Questo comportamento viene descritto nel concetto di potenziale d'azione.

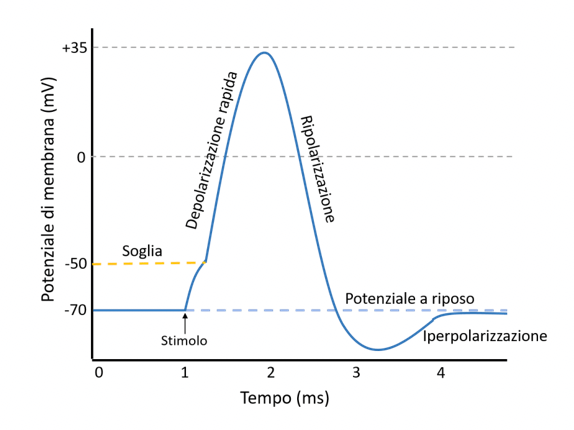
L'immagine descrive l'attivazione di un neurone naturale. La depolarizzazione fa attivare il neurone, descritta in millivolt, e durante il suo periodo di "ricarica", la membrana è quasi isolata da ulteriori riattivazioni.

Sia i neuroni artificiali che quelli umani operano come unità di base in una rete più ampia, elaborando e trasmettendo informazioni. Tuttavia, le modalità con cui avviene questo processo sono fondamentalmente diverse.

La capacità di apprendimento e adattamento è un aspetto che distingue notevolmente i due tipi di neuroni. Mentre il cervello umano può formare nuove connessioni e modificare quelle esistenti attraverso la plasticità sinaptica, le reti neurali artificiali imitano questo processo in modo più limitato, regolando i pesi durante l'addestramento.

Questo non cattura la piena gamma di adattabilità e apprendimento del cervello umano, che può riconfigurarsi in risposta a un'ampia varietà di stimoli e esperienze.

In termini di efficienza e complessità, il cervello umano si distingue per la sua capacità di gestire compiti di grande complessità con un consumo energetico sorprendentemente basso.

Al contrario, le reti neurali artificiali, soprattutto quelle impegnate in attività computazionalmente intense come il riconoscimento di immagini o il processamento del linguaggio naturale, possono richiedere risorse computazionali ingenti. Basti pensare agli enormi supercomputer usati da OpenAI e Google per addestrare i modelli come ChatGPT e Gemini rispettivamente

Il cervello umano è incredibilmente più efficiente rispetto alle reti neurali artificiali più performanti del momento grazie alla sua abilità di lavorare a pieno regime consumando un numero limitato di risorse

Inoltre, il cervello umano possiede capacità come intuizione, emozione e decisioni basate su stimoli sensoriali e cognitivi diversificati, aspetti che rimangono una sfida per l'intelligenza artificiale.

‍Come impara una rete neurale?

Le reti neurali sono considerate delle black box (scatola chiusa) - non sappiamo perché raggiungano queste performance, ma sappiamo come lo fanno.

I cosiddetti dense layers (strati densi), che sono gli strati più comuni in una rete neurale, creano interconnessioni tra i vari strati della rete.

Ogni neurone è connesso ad ogni altro neurone dello strato successivo, il che significa che il suo valore di output diventa l'input per i prossimi neuroni.

Ogni connessione tra neuroni possiede un peso (weight) che è uno dei fattori che viene modificato durante l'addestramento. Il peso della connessione influenza quanto input viene passato tra un neurone all'altro. Questo comportamento segue la formula \( inputs \times weights \).

Una volta che un neurone riceve gli input da tutti gli altri neuroni connessi ad esso, viene aggiunto un bias, un valore costante che va sommato al calcolo che coinvolge il peso menzionato. Anche il bias è un fattore che viene modificato durante l'addestramento.

L'output di un neurone è espresso dalla formula \( output = inputs \times weights + bias \).

L'aggiustamento di pesi e bias viene fatto nelle hidden layers (strati nascosti), che sono gli strati presenti tra lo strato di input e quello di output. Sono detti "nascosti" proprio perché non vediamo il comportamento di aggiustamento di pesi e bias.

La caratteristica che rende complesse le reti neurali è proprio la enorme mole di calcoli che avviene a livello sia di rete che di singolo neurone.

Insieme ai pesi e bias ci sono le funzioni di attivazione che aggiungono una ulteriore complessità matematica ma influenzano enormemente la performance di una rete neurale.

Deep Learning with Python (seconda edizione) da F. Chollet

Una bibbia del deep learning in Python da uno degli esponenti del settore

Compralo su Amazon

Pesi e bias possono essere interpretati come un sistema di manopole che possiamo ruotare per ottimizzare il nostro modello - come quando cerchiamo di sintonizzare la nostra radio ruotando le manopole per cercare la frequenza gradita.

La differenza sostanziale è che in una rete neurale, abbiamo centinaia se non migliaia di manopole da girare per raggiungere il risultato finale.

Poiché pesi e bias sono dei parametri della rete, questi saranno oggetto del cambiamento generato dalla rotazione della manopola immaginaria.

Visto che i pesi sono moltiplicati all'input, questi influenzano la magnitudine dell'input. Il bias, invece, poiché è sommato all'espressione \( inputs \times weights \), sposterà la funzione nel piano dimensionale. Vediamo degli esempi.

Ricordiamo che la formula è \( output = inputs \times weights + bias \)

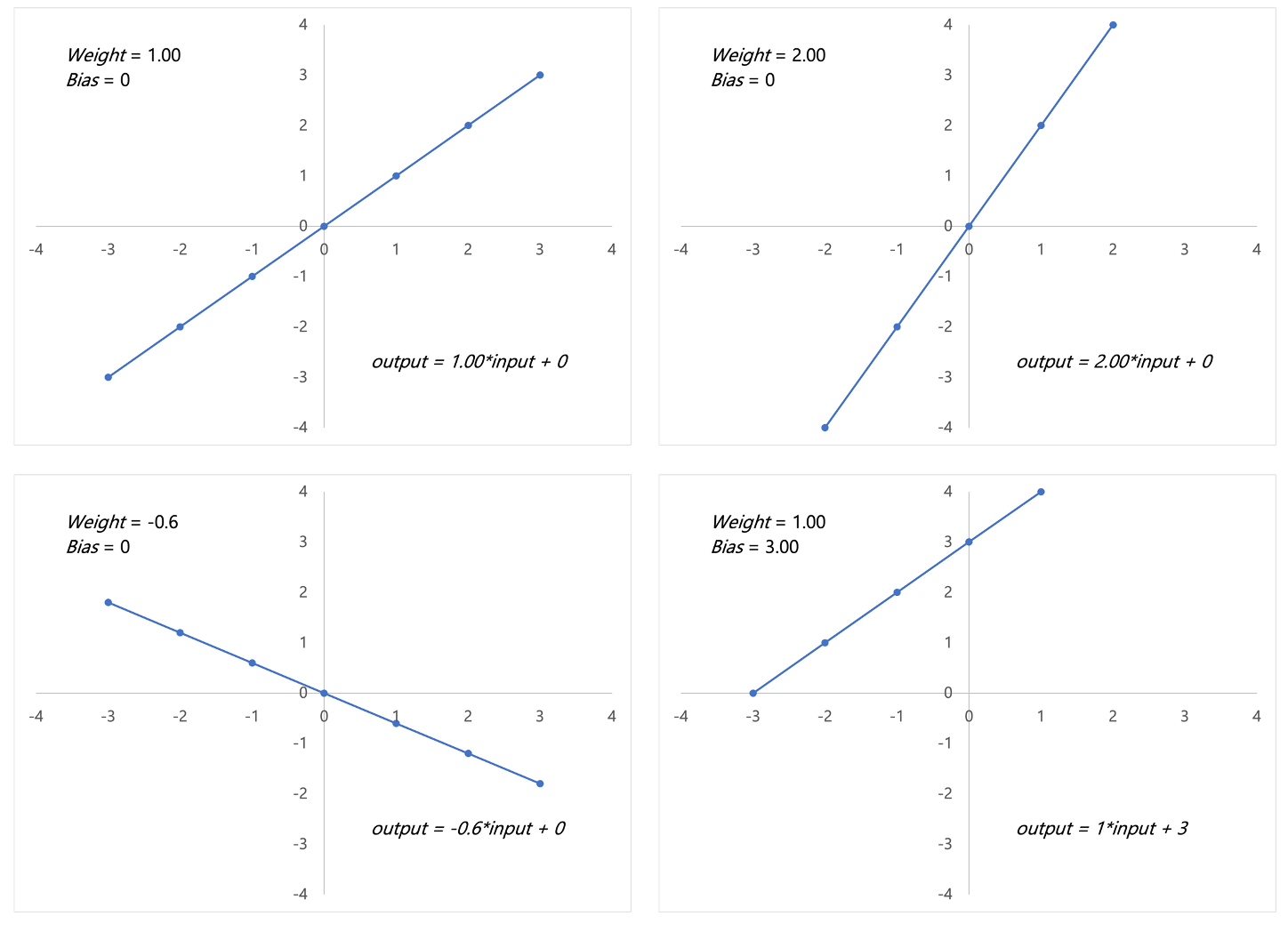
Com'è possibile notare, pesi e bias impattano il comportamento di ogni neurone artificiale, ma lo fanno in maniera rispettivamente diversa. I pesi sono solitamente inizializzati casualmente mentre il bias a 0.

‍Il comportamento di un neurone è anche influenzato dalla sua funzione di attivazione che, parallela al potenziale d'azione per un neurone naturale, definisce le condizioni di attivazione e relativi valori dell'output finale.

Funzioni di attivazione

Il tema delle funzioni di attivazione merita un articolo a sé, ma qui presenterò una overview generale.

Se ricordate, ho menzionato come un neurone naturale abbia una attivazione a switch. In gergo informatico/matematico, chiamiamo questa funzione una step function (funzione gradino).

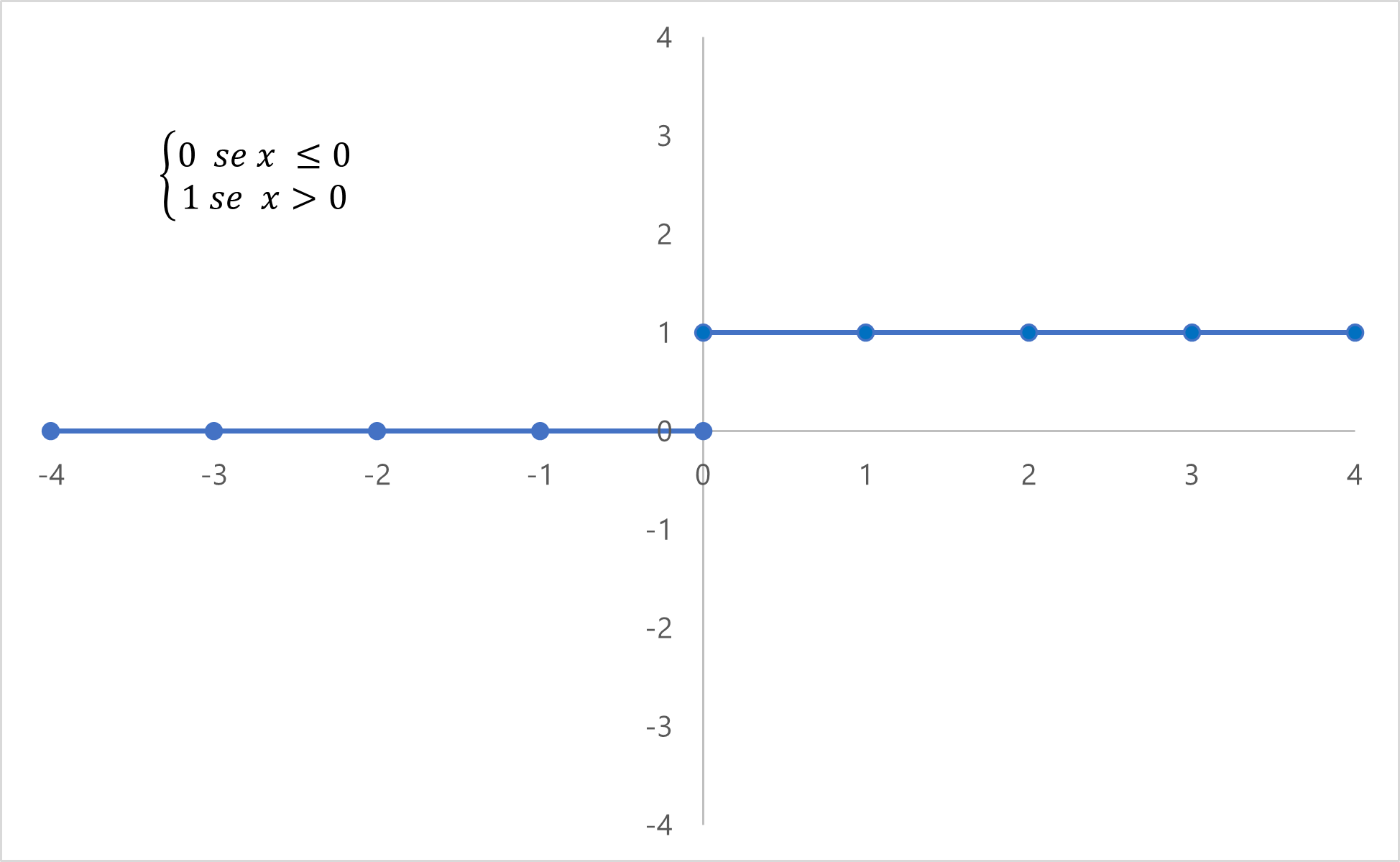
Seguendo la logica

\( 1 \ x > 0; 0 \ x \leq 0 \)

la funzione gradino permette al neurone di restituire 1 se l'input è maggiore di 0 oppure 0 se l'input è minore o uguale a 0. Questo comportamento simula il comportamento di un neurone naturale e segue la formula

\( output = sum(inputs \times weights) + bias \)

La step function è però molto semplice, e nel settore si tende ad usare delle funzioni di attivazione più complesse, come l'unità lineare rettificata (ReLU) e SoftMax.

Questa immagine mette insieme tutti i pezzi, mostrando i calcoli interni che fa un neurone artificiale, da input a output.

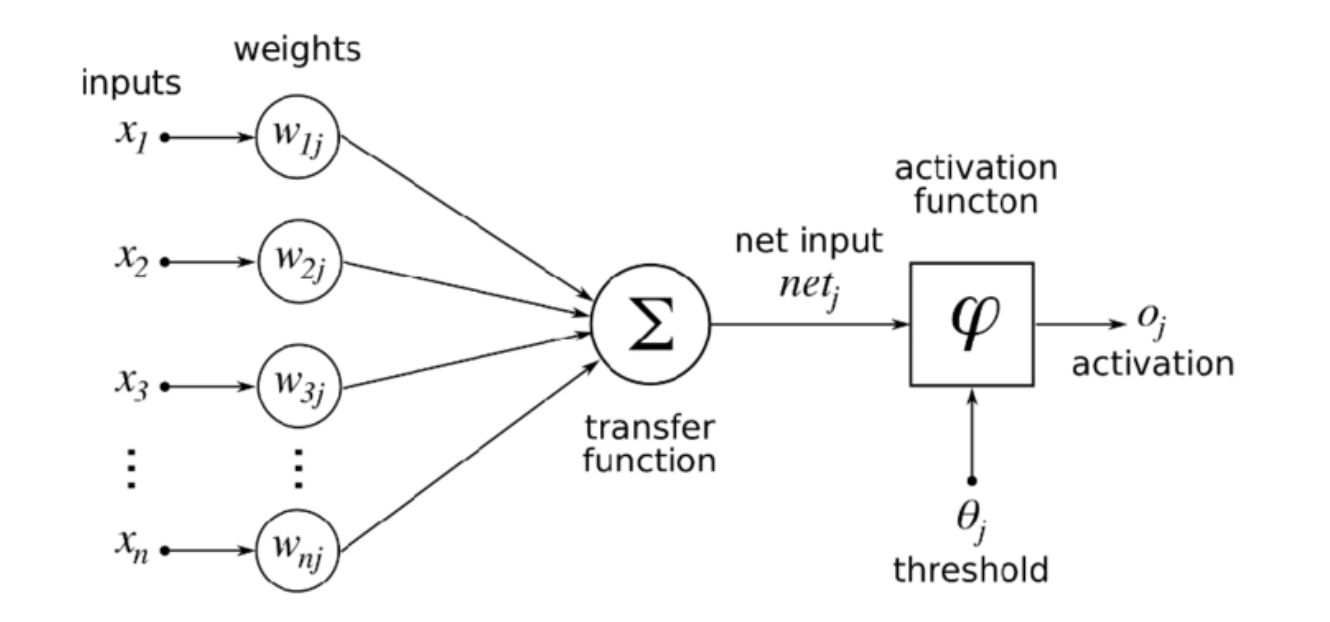
Come scrivere una piccola rete in Python

Creemo una piccola rete neurale con 4 input e 3 neuroni per comprendere come funziona il calcolo di pesi e bias.

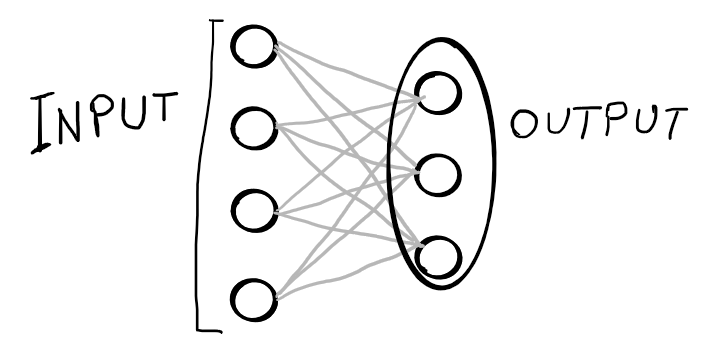
Iniziamo dal definire questi parametri manualmente a scopo d'esempio

inputs = [1, 2, 3, 4] # quattro input
# weights è un array 3x4 -> 3 neuroni, 4 pesi associati ad ogni connessione
weights = [[ 0.74864643, -1.00722027,  1.45983017,  1.34236011],
           [-1.20116017, -0.08884298, -0.46555646,  0.02341039],
           [-0.30973958,  0.89235565, -0.92841053,  0.12266543]]
biases = [0, 0.3, -0.5] # ogni neurone ha un bias

Ora creiamo il loop che andrà a creare la nostra piccola rete neurale

layer_outputs = [] # creiamo la lista che conterrà i risultati dell'elaborazione dei neuroni dello strato 
# per ogni neurone
for neuron_weights, neuron_bias in zip(weights, biases):
    # inizializziamo l'output a 0
    neuron_output = 0
    # per ogni input e peso
    for n_input, weight in zip(inputs, neuron_weights):
        # moltiplicare input e peso e aggiungerlo all'output
        neuron_output += n_input * weight
    # aggiungere il bias all'output
    neuron_output += neuron_bias
    # aggiungere il risultato del neurone allo strato
    layer_outputs.append(neuron_output)

print(layer_outputs) # stampiamo il risultato

L'output finale è questo

Codice completo

inputs = [1, 2, 3, 4] # quattro input
# weights è un array 3x4 -> 3 neuroni, 4 pesi associati ad ogni connessione
weights = [[ 0.74864643, -1.00722027,  1.45983017,  1.34236011],
           [-1.20116017, -0.08884298, -0.46555646,  0.02341039],
           [-0.30973958,  0.89235565, -0.92841053,  0.12266543]]
biases = [0, 0.3, -0.5] # ogni neurone ha un bias

layer_outputs = [] # creiamo la lista che conterrà i risultati dell'elaborazione dei neuroni dello strato 
# per ogni neurone
for neuron_weights, neuron_bias in zip(weights, biases):
    # inizializziamo l'output a 0
    neuron_output = 0
    # per ogni input e peso
    for n_input, weight in zip(inputs, neuron_weights):
        # moltiplicare input e peso e aggiungerlo all'output
        neuron_output += n_input * weight
    # aggiungere il bias all'output
    neuron_output += neuron_bias
    # aggiungere il risultato del neurone allo strato
    layer_outputs.append(neuron_output)

print(layer_outputs) # stampiamo il risultato