Tabella dei Contenuti
Il TF-IDF è una tecnica di vettorizzazione molto conosciuta e documentata nel data science. La vettorizzazione è l'atto di convertire un dato in un formato numerico in modo tale che un modello statistico possa interpretarlo e fare le predizioni.
In questo articolo vedremo come convertire un corpus di testi in formato numerico e applicheremo degli algoritmi di apprendimento automatico per far emergere pattern e anomalie interessanti.
Metodologia
Utilizzeremo un dataset fornito da Sklearn per avere un corpus di testo replicabile. Dopodiché, useremo l'algoritmo KMeans per raggruppare i vettori generati dal TF-IDF.
Useremo poi la Principal Component Analysis per visualizzare i nostri gruppi e far emergere caratteristiche comuni o inusuali dei testi presenti nel nostro corpus.
Ecco una scaletta
- Importiamo il dataset
- Applichiamo preprocessing al nostro corpus, così da rimuovere parole e simboli che, se convertiti in formato numerico, non aggiungono valore al nostro modello
- Usiamo il TF-IDF come algoritmo di vettorizzazione
- Applichiamo KMeans per raggruppare i nostri dati
- Applichiamo PCA per ridurre la dimensionalità dei nostri vettori a 2 per visualizzazione
- Interpreteremo i dati e inseriremo le nostre considerazioni in un report finale
- Preprocessare un corpus di testi per prepararli alla vettorizzazione
- Applicare l'algoritmo TF-IDF sui testi in modo da convertirli in formato numerico
- Applicare il clustering K-Means per trovare gruppi di testi simili
- Applicare la PCA per visualizzare i raggruppamenti in 2 dimensioni
L'Analisi
Il Dataset
Per questo esempio useremo l'API di Scikit-Learn, sklearn.datasets che permette di accedere ad un famoso dataset per analisi linguistiche, il 20 newsgroups. Un newsgroup è un gruppo di discussione di utenti online, ad esempio un forum. Sklearn permette di accedere a diverse categorie di contenuto. Useremo i testi che hanno a che vedere con la tecnologia, la religione e lo sport.
# importiamo le librerie necessarie da sklearn
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
# importiamo le altre librerie necessarie
import pandas as pd
import numpy as np
# librerie per la manipolazione del testo
import re
import string
import nltk
from nltk.corpus import stopwords
# importiamo le librerie di visualizzazione
import matplotlib.pyplot as plt
categories = [
'comp.graphics',
'comp.os.ms-windows.misc',
'rec.sport.baseball',
'rec.sport.hockey',
'alt.atheism',
'soc.religion.christian',
]
dataset = fetch_20newsgroups(subset='train', categories=categories, shuffle=True, remove=('headers', 'footers', 'quotes'))Se accediamo al primo elemento con dataset['data'][0] vediamo
They tried their best not to show it, believe me. I'm surprised they couldn't find a sprint car race (mini cars through pigpens, indeed!) on short notice.
George
È possibile che il vostro dato sia diverso a causa del shuffle=True, che randomizza l'ordine degli elementi del dataset. Il numero di elementi nel nostro dataset è 3451.
Creiamo un dataframe Pandas dal nostro dataset
df = pd.DataFrame(dataset.data, columns=["corpus"])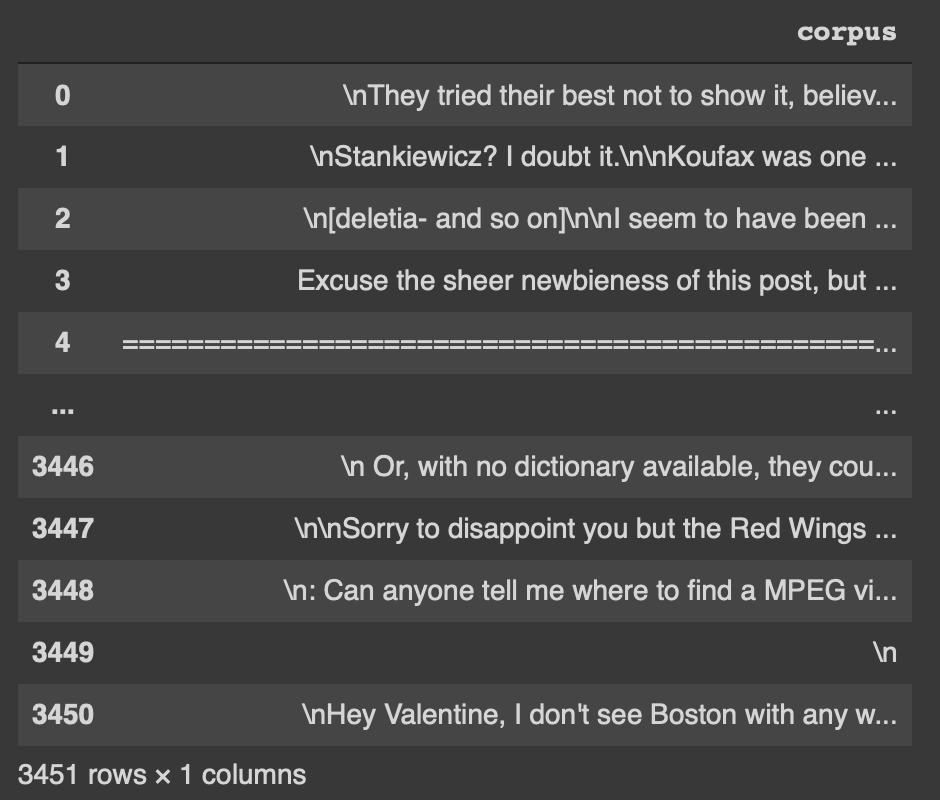
Notiamo come siano presenti "\n", "===" e altri simboli che andrebbero rimossi per addestrare correttamente il nostro modello.
Machine Learning Engineering
Andriy Burkov
Questo è IL libro di IA applicata più completo in circolazione. È pieno di best practice e modelli di progettazione per la creazione di soluzioni di apprendimento automatico affidabili e scalabili.
Preprocessing
Insieme ai simboli menzionati, vogliamo anche le stopword. Quest'ultime sono una serie di parole che non aggiungono informazioni al nostro modello. Un esempio di stopword in inglese sono gli articoli, le congiunzioni e così via.
Useremo la libreria NLTK e importiamo le stopword per visualizzarle
import nltk
from nltk.corpus import stopwords
# nltk.download('stopwords')
stopwords.words("english")[:10] # <-- importiamo le stopword inglesi>>> ['i', 'me', 'my', 'myself', 'we', 'our', 'ours', 'ourselves', 'you', "you're"]
Ora creiamo una funzione preprocess_text che prende in input un testo e restituisce una versione pulita dello stesso.
def preprocess_text(text: str, remove_stopwords: bool) -> str:
"""Funzione che pulisce il testo in input andando a
- rimuovere i link
- rimuovere i caratteri speciali
- rimuovere i numeri
- rimuovere le stopword
- trasformare in minuscolo
- rimuovere spazi bianchi eccessivi
Argomenti:
text (str): testo da pulire
remove_stopwords (bool): rimuovere o meno le stopword
Restituisce:
str: testo pulito
"""
# rimuovi link
text = re.sub(r"http\S+", "", text)
# rimuovi numeri e caratteri speciali
text = re.sub("[^A-Za-z]+", " ", text)
# rimuovere le stopword
if remove_stopwords:
# 1. crea token
tokens = nltk.word_tokenize(text)
# 2. controlla se è una stopword
tokens = [w for w in tokens if not w.lower() in stopwords.words("english")]
# 3. unisci tutti i token
text = " ".join(tokens)
# restituisci il testo pulito, senza spazi eccessivi, in minuscolo
text = text.lower().strip()
return textEcco un lo stesso documento precedente, stavolta pulito
tried best show believe im surprised couldnt find sprint car race mini cars pigpens indeed short notice george
Applichiamo la funzione a tutto il dataframe
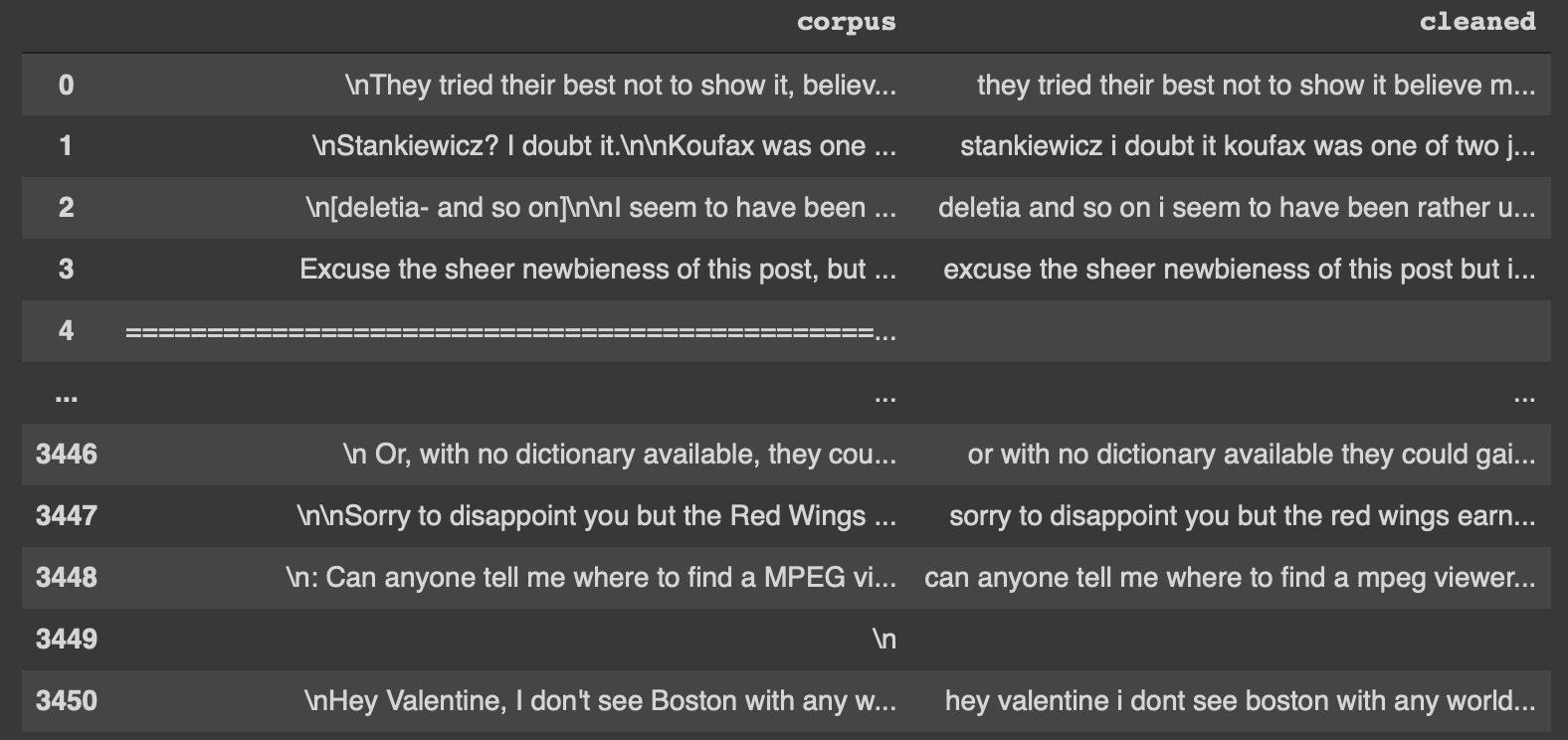
Ora siamo pronti alla vettorizzazione.
Vettorizzazione con TF-IDF
Il TF-IDF converte in un formato numerico il nostro corpus facendo emergere termini specifici, pesando diversamente i termini molto rari o molto comuni in modo da assegnare loro un punteggio basso.
TF sta per term frequency, mentre IDF sta per inverse document frequency. Il valore TF-IDF aumenta proporzionalmente al numero di volte che una parola appare nel documento ed è compensato dal numero di documenti nel corpus che contengono quella parola.
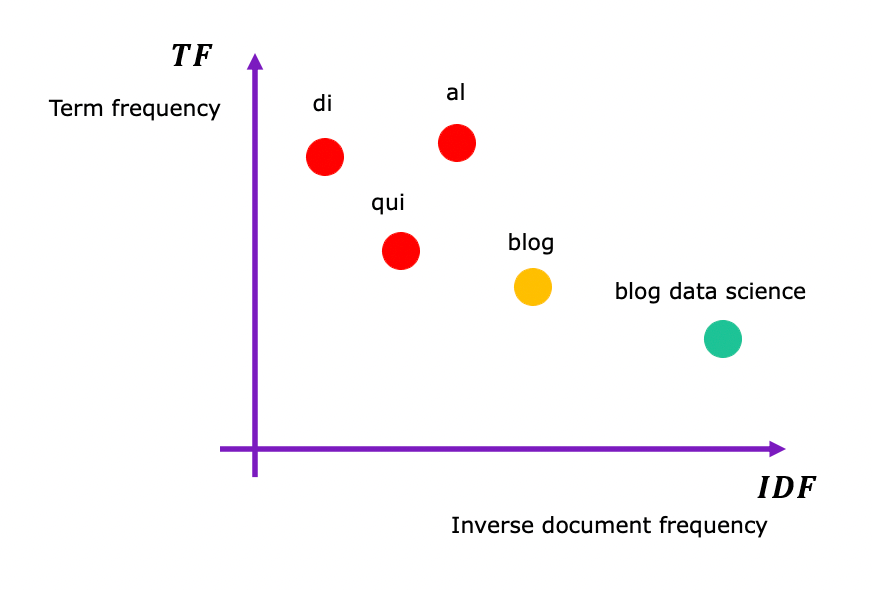
Con questa tecnica di vettorizzazione siamo quindi in grado di raggruppare i nostri documenti considerando i termini più importanti che li costituiscono. Per leggere di più su come funziona il TF-IDF, leggere qui.
È facile applicare il TF-IDF con Sklearn:
# inizializziamo il vettorizzatore
vectorizer = TfidfVectorizer(sublinear_tf=True, min_df=5, max_df=0.95)
# fit_transform applica il TF-IDF ai testi puliti - salviamo la matrice di vettori in X
X = vectorizer.fit_transform(df['cleaned'])X è la matrice di vettori che verrà usata per addestrare il modello KMeans. Il comportamento predefinito di Sklearn è quello di creare una matrice sparsa. La vettorizzazione genera dei vettori simili a questo
vettore_a = [1.204, 0, 0, 0, 0, 0, 0, ..., 0]
Il vettore è composto da un singolo valore non uguale a 0. In Sklearn, una matrice sparsa non è altro che una matrice che indicizza la posizione dei valori e degli 0 invece di memorizzarla come una qualsiasi altra matrice. Questo è un meccanismo che serve a risparmiare RAM e potenza di calcolo. La comodità è che la matrice sparsa è accettata dalla maggior parte degli algoritmi di machine learning, come anche il KMeans. Infatti quest'ultimo userà i dati presenti nella matrice sparsa per trovare gruppi e pattern.
Se usiamo X.toarray() vediamo di fatto la matrice completa, non sparsa.

Implementazione del KMeans
Il KMeans è uno degli algoritmi non supervisionati più conosciuti e usati nel mondo del data science e serve a raggruppare in un numero definito di gruppi un insieme di dati. L'idea alla base è molto semplice: l'algoritmo inizializza delle posizioni a caso (chiamati centroidi, i punti rossi, blu e verdi nello screenshot in basso) nel piano vettoriale e assegna il punto al centroide più vicino.
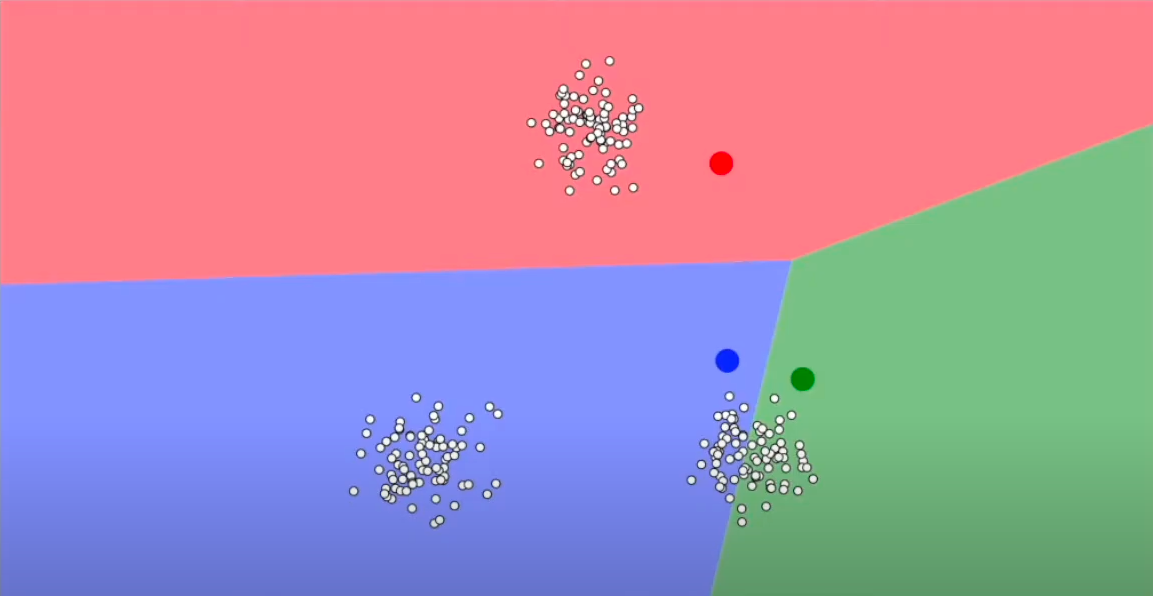
L'algoritmo calcola la posizione media (o, se aiuta l'interpretazione, il "centro di gravità") dei punti e sposta il rispettivo centroide in quella posizione e aggiorna il gruppo di appartenenza di ogni punto. L'algoritmo converge quando tutti i punti sono alla distanza minima dal rispettivo centroide.
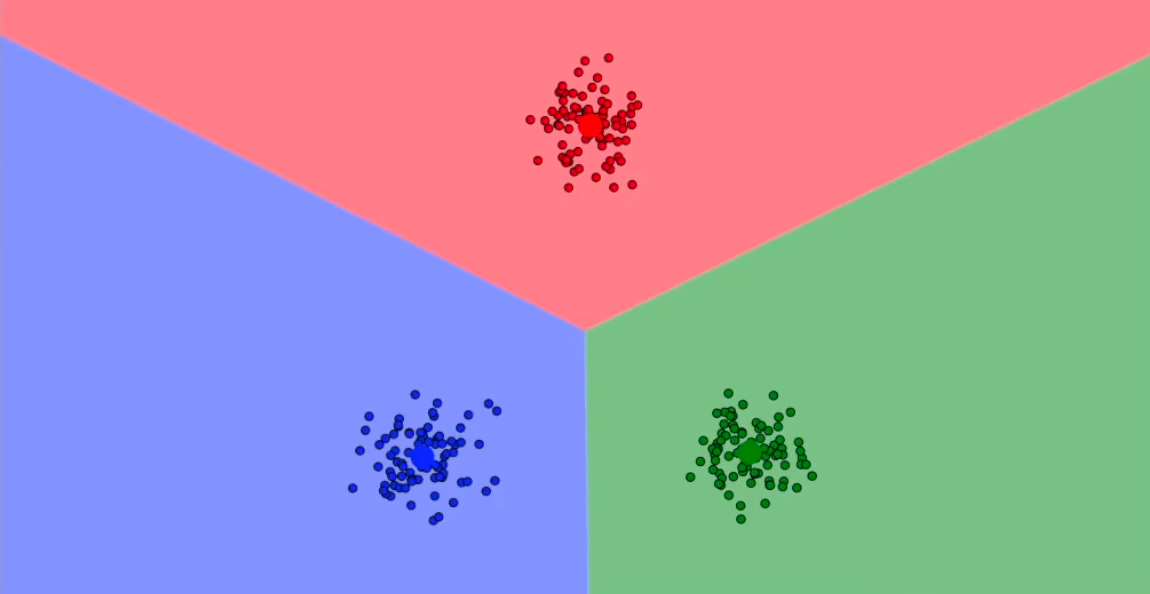
Fatta questa doverosa introduzione, continuiamo con il nostro progetto andando a usare nuovamente Sklearn
from sklearn.cluster import KMeans
# inizializziamo il kmeans con 3 centroidi
kmeans = KMeans(n_clusters=3, random_state=42)
# addestriamo il modello
kmeans.fit(X)
# salviamo i gruppi di ogni punto
clusters = kmeans.labels_Con questo snippet di codice abbiamo addestrato il KMeans con i vettori restituiti dal TF-IDF e abbiamo assegnato i gruppi che ha trovato ad alla variabile clusters
Ora possiamo procedere alla visualizzazione dei nostri gruppi e valutare la loro segmentazione e/o presenza di anomalie.
Riduzione della dimensionalità e visualizzazione
Abbiamo la nostra X dal TF-IDF e abbiamo un modello KMeans e relativi cluster. Ora vogliamo mettere insieme questi due pezzi per visualizzare in quale gruppo va quale testo.
Come ben sappiamo, un grafico si presenta solitamente in 2 dimensioni e raramente in 3. Sicuramente non possiamo visualizzarne di più. Se andiamo a vedere la dimensionalità di X con X.shape vediamo che essa è (3451, 7390). Ci sono 3451 vettori (uno per testo), ognuno con 7390 dimensioni. Impossibile visualizzarle!
Fortunatamente per noi, esiste una tecnica che si chiama PCA (Principal Component Analysis) che riduce la dimensionalità di un set di dati ad un numero arbitrario preservando la maggior parte delle informazioni contenute in esse.
Come per il TF-IDF, non andrò nel dettaglio del suo funzionamento, e potete leggere di più qui sul suo funzionamento. Al fine di questo articolo, ci basti sapere che la PCA tende a preservare le dimensioni che meglio riassumono la variabilità totale dei nostri dati, andando a rimuovere dimensioni che contribuiscono poco a quest'ultima.
La nostra X andrà da 7390 dimensioni a 2. Sklearn.decomposition.PCA è quello che ci occorre.
from sklearn.decomposition import PCA
# inizializziamo la PCA con 2 componenti
pca = PCA(n_components=2, random_state=42)
# passiamo alla pca il nostro array X
pca_vecs = pca.fit_transform(X.toarray())
# salviamo le nostre due dimensioni in x0 e x1
x0 = pca_vecs[:, 0]
x1 = pca_vecs[:, 1]
Se ora vediamo la dimensionalità di x0 e x1 vediamo che sono rispettivamente (3451,), quindi un punto (x0,x1) per testo. Questo ci da la possibilità di creare un grafico a dispersione.
Visualizzare i gruppi
Prima di creare il nostro grafico andiamo ad organizzare meglio il nostro dataframe andando a creare una colonna cluster, x0, x1
# assegnamo cluster e vettori PCA a delle colonne nel dataframe originale
df['cluster'] = clusters
df['x0'] = x0
df['x1'] = x1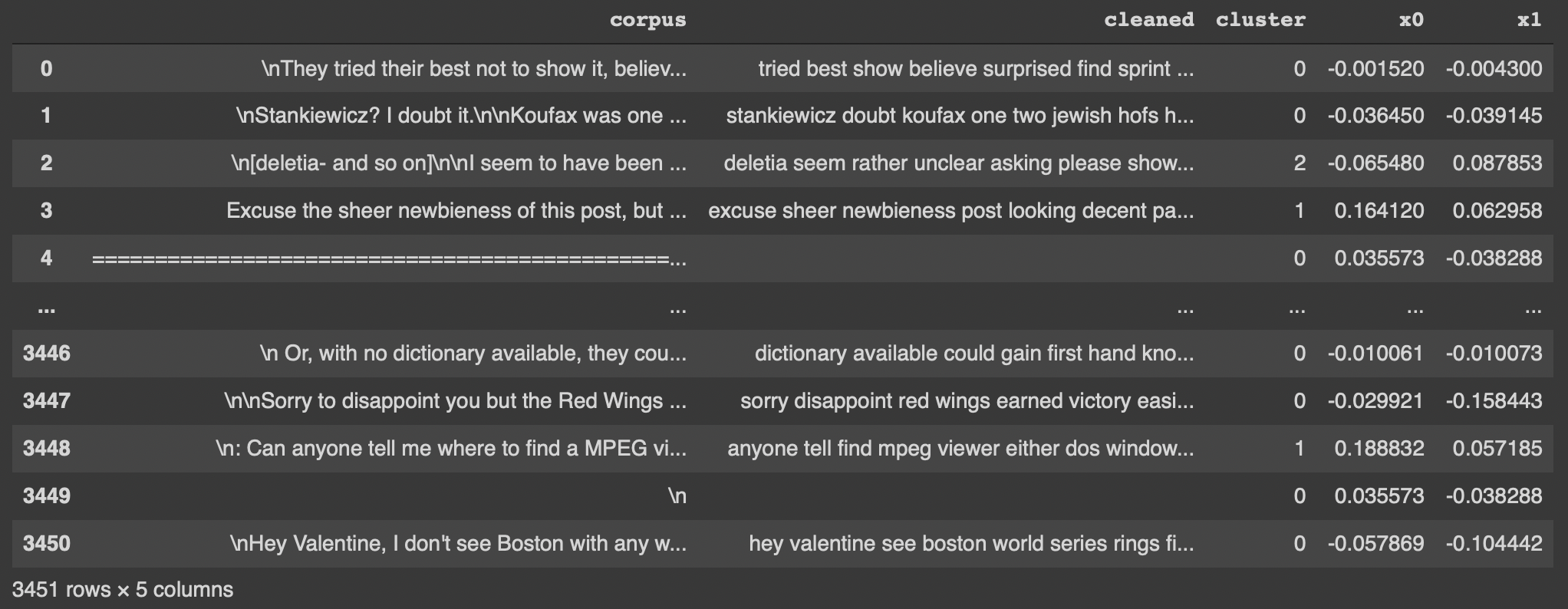
Vediamo quali sono le keyword più rilevanti per ogni centroide
def get_top_keywords(n_terms):
"""Questa funzione restituisce le keyword per ogni centroide del KMeans"""
df = pd.DataFrame(X.todense()).groupby(clusters).mean() # raggruppa il vettore TF-IDF per gruppo
terms = vectorizer.get_feature_names_out() # accedi ai termini del tf idf
for i,r in df.iterrows():
print('\nCluster {}'.format(i))
print(','.join([terms[t] for t in np.argsort(r)[-n_terms:]])) # per ogni riga del dataframe, trova gli n termini che hanno il punteggio più alto
get_top_keywords(10)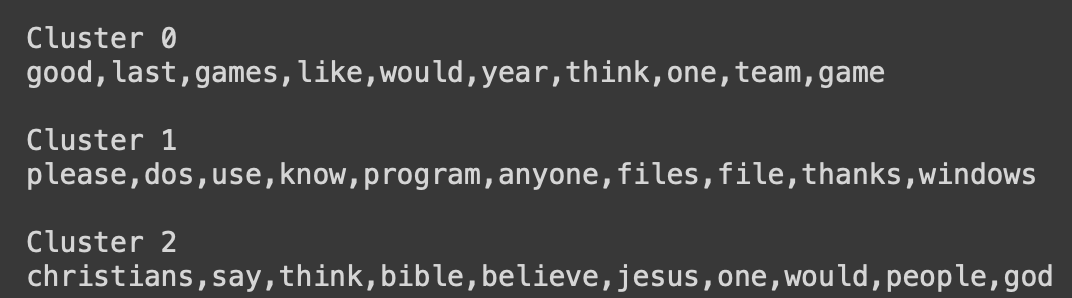
Bene! Vediamo come il KMeans abbia correttamente creato 3 gruppi distinti, uno per ogni categoria presente nel dataset. Il cluster 0 si riferisce allo sport, il cluster 2 al software / tech, il cluster 3 alla religione. Applichiamo questa mappatura
# mappiamo cluster con termini adatti
cluster_map = {0: "sport", 1: "tecnologia", 2: "religione"}
# applichiamo mappatura
df['cluster'] = df['cluster'].map(cluster_map)Procediamo con la libreria Seaborn per visualizzare in maniera molto semplice i nostri testi raggruppati.
# settiamo la grandezza dell'immagine
plt.figure(figsize=(12, 7))
# settiamo titolo
plt.title("Raggruppamento TF-IDF + KMeans 20newsgroup", fontdict={"fontsize": 18})
# settiamo nome assi
plt.xlabel("X0", fontdict={"fontsize": 16})
plt.ylabel("X1", fontdict={"fontsize": 16})
# creiamo diagramma a dispersione con seaborn, dove hue è la classe usata per raggruppare i dati
sns.scatterplot(data=df, x='x0', y='x1', hue='cluster', palette="viridis")
plt.show()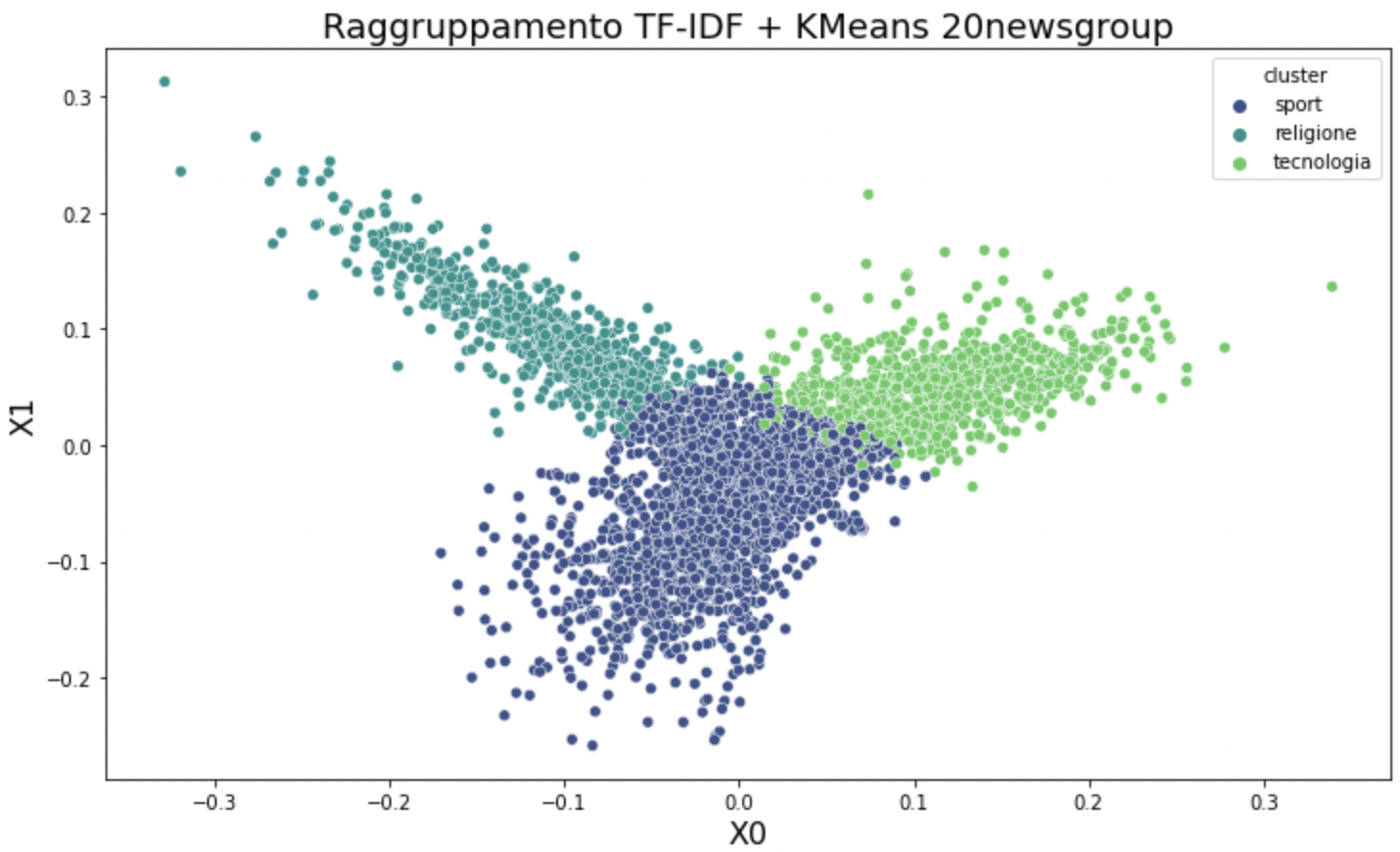
Come è possibile vedere, il clustering ha funzionato bene: tre gruppi distinti come lo sono i gruppi definiti a priori dal nostro dataset. Immaginate la potenza di questo approccio nel trovare gruppi in dati non etichettati a priori!
Interpretazione
L'interpretazione è abbastanza semplice: non sono presenti anomalie particolari, tranne per il fatto che ci sono dei testi appartenenti alla categoria tecnologia che si mischiano leggermente con quelli dello sport, tra il confine blu scuro e verde acceso. Questo è dovuto alla presenza di termini comuni tra alcuni di questi testi che quando vettorizzati ottengono valori uguali per alcune dimensioni.
Come follow-up sarebbe interessante andare ad investigare come sono scritti questi testi e capire se la motivazione ipotizzata sia fondata o meno.
Il codice
Ecco tutto il codice completo, in formato copia-incolla
def preprocess_text(text: str, remove_stopwords: bool) -> str:
"""Funzione che pulisce il testo in input andando a
- rimuovere i link
- rimuovere i caratteri speciali
- rimuovere i numeri
- rimuovere le stopword
- trasformare in minuscolo
- rimuovere spazi bianchi eccessivi
Argomenti:
text (str): testo da pulire
remove_stopwords (bool): rimuovere o meno le stopword
Restituisce:
str: testo pulito
"""
# rimuovi link
text = re.sub(r"http\S+", "", text)
# rimuovi numeri e caratteri speciali
text = re.sub("[^A-Za-z]+", " ", text)
# rimuovere le stopword
if remove_stopwords:
# 1. crea token
tokens = nltk.word_tokenize(text)
# 2. controlla se è una stopword
tokens = [w for w in tokens if not w.lower() in stopwords.words("english")]
# 3. unisci tutti i token
text = " ".join(tokens)
# restituisci il testo pulito, senza spazi eccessivi, in minuscolo
text = text.lower().strip()
return text
def get_top_keywords(n_terms):
"""Questa funzione restituisce le keyword per ogni centroide del KMeans"""
df = pd.DataFrame(X.todense()).groupby(clusters).mean() # raggruppa il vettore TF-IDF per gruppo
terms = vectorizer.get_feature_names_out() # accedi ai termini del tf idf
for i,r in df.iterrows():
print('\nCluster {}'.format(i))
print(','.join([terms[t] for t in np.argsort(r)[-n_terms:]])) # per ogni riga del dataframe, trova gli n termini che hanno il punteggio più alto# importiamo le librerie necessarie da sklearn
from sklearn.datasets import fetch_20newsgroups
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.cluster import KMeans
from sklearn.decomposition import PCA
# importiamo le altre librerie necessarie
import pandas as pd
import numpy as np
# librerie per la manipolazione del testo
import re
import string
import nltk
nltk.download('punkt')
nltk.download('stopwords')
from nltk.corpus import stopwords
# librerie di visualizzazione
import matplotlib.pyplot as plt
import seaborn as sns
categories = [
'comp.graphics',
'comp.os.ms-windows.misc',
'rec.sport.baseball',
'rec.sport.hockey',
'alt.atheism',
'soc.religion.christian',
]
dataset = fetch_20newsgroups(subset='train', categories=categories, shuffle=True, remove=('headers', 'footers', 'quotes'))
df = pd.DataFrame(dataset.data, columns=["corpus"])
df['cleaned'] = df['corpus'].apply(lambda x: preprocess_text(x, remove_stopwords=True))
# inizializziamo il vettorizzatore
vectorizer = TfidfVectorizer(sublinear_tf=True, min_df=5, max_df=0.95)
# fit_transform applica il TF-IDF ai testi puliti - salviamo la matrice di vettori in X
X = vectorizer.fit_transform(df['cleaned'])
# inizializziamo il KMeans con 3 cluster
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X)
clusters = kmeans.labels_
# inizializziamo la PCA con 2 componenti
pca = PCA(n_components=2, random_state=42)
# passiamo alla pca il nostro array X
pca_vecs = pca.fit_transform(X.toarray())
# salviamo le nostre due dimensioni in x0 e x1
x0 = pca_vecs[:, 0]
x1 = pca_vecs[:, 1]
# assegnamo cluster e vettori PCA a delle colonne nel dataframe originale
df['cluster'] = clusters
df['x0'] = x0
df['x1'] = x1
cluster_map = {0: "sport", 1: "tecnologia", 2: "religione"} # mappatura trovata con get_top_keywords
df['cluster'] = df['cluster'].map(cluster_map)
# settiamo la grandezza dell'immagine
plt.figure(figsize=(12, 7))
# settiamo titolo
plt.title("Raggruppamento TF-IDF + KMeans 20newsgroup", fontdict={"fontsize": 18})
# settiamo nome assi
plt.xlabel("X0", fontdict={"fontsize": 16})
plt.ylabel("X1", fontdict={"fontsize": 16})
# creiamo diagramma a dispersione con seaborn, dove hue è la classe usata per raggruppare i dati
sns.scatterplot(data=df, x='x0', y='x1', hue='cluster', palette="viridis")
plt.show()







Commenti dalla community