Il Machine Learning è una disciplina che sta avendo un enorme sviluppo in ambito tecnologico e industriale.
Grazie ai suoi algoritmi e alle sue tecniche di modellazione, è possibile costruire modelli in grado di apprendere da dati passati, generalizzare e fare previsioni su nuovi dati.
Tuttavia, in alcuni casi, i modelli possono adattarsi troppo ai dati di addestramento e perdere la loro capacità di generalizzazione. Questo fenomeno si chiama overfitting.
È importante per gli addetti ai lavori comprendere cosa sia l'overfitting e perché rappresenta uno degli ostacoli principali nel Machine Learning per quando riguarda la creazione di un modello predittivo.
Quando un modello è troppo complesso o si adatta troppo bene ai dati di addestramento, può diventare molto preciso per quei dati specifici, ma generalizzerà male su dati che non ha mai visto prima. Ciò significa che il modello sarà inefficace quando si applica a nuovi dati nella realtà.
Per prevenire l'overfitting è possibile utilizzare tecniche di regolarizzazione.
Il termine regolarizzazione fa da cappello ad un insieme di tecniche che semplificano un modello predittivo. In questo articolo, ci concentreremo su due tecniche di regolarizzazione, L1 e L2, spiegandone le differenze e illustrando come applicarle in Python.
Cos'è la regolarizzazione e perché è importante?
In termini semplici, regolarizzare un modello significa cambiare il suo comportamento di apprendimento durante la fase di addestramento.
La regolarizzazione aiuta a prevenire l'overfitting aggiungendo una penalità sulla complessità del modello - se un modello è troppo complesso, verrà penalizzato durante l'addestramento, il che aiuta a mantenere un buon bilanciamento tra la complessità del modello e la sua capacità di generalizzare su dati che non ha mai visto prima.
Per aggiungere una regolarizzazione L1 o L2, andiamo ad alterare la funzione di perdita (loss function in inglese) del modello. Questa è l'espressione che l'algoritmo di apprendimento cerca di ottimizzare durante la fase di addestramento.
La regolarizzazione avviene assegnando una penalità che aumenta in base a quanto complesso diventa il modello.
Se prendiamo la regressione lineare come esempio, vediamo come la tipica loss function del MSE (mean squared error - leggi di più sulle metriche di valutazione di un modello di regressione qui) possa essere espressa così
\[ min_{w^{(i)}} \lbrack \frac{1}{N} \times{\sum_{i=1}^{N} (f(x_{i}) - y)^2} \rbrack \]
Dove l'obiettivo dell'algoritmo è quello di minimizzare la differenza tra la predizione \( f(x) \) e la \(y \) reale.
Nella equazione, \( f(x) \) è la linea di regressione, e questa avrà forma
\[ f = w^{(i)} x^{(i)} + b\]
L'algoritmo quindi dovrà trovare i valori dei parametri \( w \) e \( b \) dal set di addestramento andando a minimizzare MSE.
Un modello è considerato meno complesso se alcuni parametri \( w \) sono vicini o uguali a zero.
Regolarizzazione L1 vs L2
Vediamo ora le differenze tra regolarlizzazione L1 e L2.
Regolarizzazione L1
La regolarizzazione L1, anche conosciuta come "Lasso", aggiunge una penalità sulla somma degli valori assoluti dei pesi del modello.
Questo significa che i pesi che non contribuiscono molto al modello saranno azzerati, il che può portare ad una selezione delle feature automatica (in quanto i pesi corrispondenti alle feature meno importanti saranno di fatto azzerati).
Questo rende L1 particolarmente utile per problemi di feature selection e modelli sparsi.
Prendendo in esempio la formula del MSE di prima, questa apparirebbe così
\[ min_{w^{(i)}} \lbrack C \times{ (\sum_{i=1}^{N} {|w^{(i)}|})} + \frac{1}{N} \times{\sum_{i=1}^{N} (f(x_{i}) - y)^2} \rbrack \]
dove \( C \) è un iperparametro del modello che controlla l'intensità della regolarizzazione. Più alto è il valore di \( C \), più i nostri pesi tenderanno verso lo zero.
In gergo, questo viene chiamato modello sparso, dove la maggior parte dei parametri ha il valore di zero.
Il rischio qui è che un valore molto alto porterà il modello all'underfitting, che è l'opposto dell'overfitting - vale a dire che non catturerà i pattern presenti nei nostri dati.
Regolarizzazione L2
D'altra parte, la regolarizzazione L2, chiamata anche regolarizzazione Ridge, somma il quadrato dei pesi al termine di regolarizzazione.
Questo significa che i pesi più grandi vengono ridotti ma non azzerati, il che porta a modelli con meno variabili rispetto alla regolarizzazione L1 ma con pesi più distribuiti.
La regolarizzazione L2 è particolarmente utile quando si hanno molte variabili altamente correlate, poiché tende a "distribuire" il peso su tutte le variabili invece di concentrarsi solo su alcune di esse.
Come prima, vediamo come l'equazione iniziale cambia per integrare L2
\[ min_{w^{(i)}} \lbrack C \times{ (\sum_{i=1}^{N} {(w^{(i)}})^{2}} + \frac{1}{N} \times{\sum_{i=1}^{N} (f(x_{i}) - y)^2} \rbrack \]
La regolarizzazione L2 può migliorare la stabilità del modello quando i dati di addestramento sono rumorosi o incompleti, poiché riduce l'impatto di valori anomali o rumore sulle variabili.
Come applicare la regolarizzazione in Sklearn e Python
In questo esempio vedremo come applicare una regolarizzazione ad un modello di regressione logistica per un problema di classificazione. Vedremo come cambiano le performance per diversi valori di \( C \) e paragoneremo quanto il modello sia accurato nel modellare i dati in input.
Useremo il famoso breast cancer dataset da Sklearn. Iniziamo a vedere come importarlo, insieme a tutte le librerie.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# importiamo il dataset da Sklearn
breast_cancer = load_breast_cancer()
# creiamo una variabile "data" che contiene il dataframe dal dataset
data = pd.DataFrame(data=breast_cancer['data'], columns=breast_cancer['feature_names'])
data['target'] = pd.Series(breast_cancer['target'], dtype='category')Essendo un problema di classifcazione, useremo la accuracy per misurare le performance del modello. Leggi l'articolo su come misurare le performance di modelli di classificazione binaria se ti interessa saperne di più.
Ora creiamo una funzione per applicare il confronto tra regolarizzazione L1 e L2 sul dataframe.
def plot_regularization(df, reg_type='l1'):
# splittiamo i nostri dati in training e test
X = df.drop('target', axis=1)
y = df['target']
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)
# definiamo i diversi valori di C
Cs = [0.001, 0.01, 0.1, 1, 10, 100, 1000]
coefs = []
test_scores = []
train_scores = []
for C in Cs:
# addestriamo il modello per i diversi valori di C
clf = LogisticRegression(penalty=reg_type, C=C, solver='liblinear')
clf.fit(X_train, y_train)
# salviamo le performance
coefs.append(clf.coef_.ravel())
train_scores.append(clf.score(X_train, y_train))
test_scores.append(clf.score(X_test, y_test))
reg = reg_type.capitalize()
# creiamo dei grafici
fig, (ax1, ax2) = plt.subplots(ncols=2, figsize=(12, 4))
ax1.plot(Cs, train_scores, 'b-o', label='Training Set')
ax1.plot(Cs, test_scores, 'r-o', label='Test Set')
plt.suptitle(f"Regolarizzazione {reg}")
ax1.set_xlabel('C')
ax1.set_ylabel('Accuracy')
ax1.set_xscale('log')
ax1.set_title('Performance')
ax1.legend()
coefs = np.array(coefs)
n_params = coefs.shape[1]
for i in range(n_params):
ax2.plot(Cs, coefs[:, i], label=X.columns[i])
ax2.axhline(y=0, linestyle='--', color='black', linewidth=2)
ax2.set_xlabel('C')
ax2.set_ylabel('Valori coefficienti')
ax2.set_xscale('log')
ax2.set_title('Coefficienti')
plt.show()Applichiamo questa logica guardando la regolarizzione L1
plot_regularization(data, 'l1')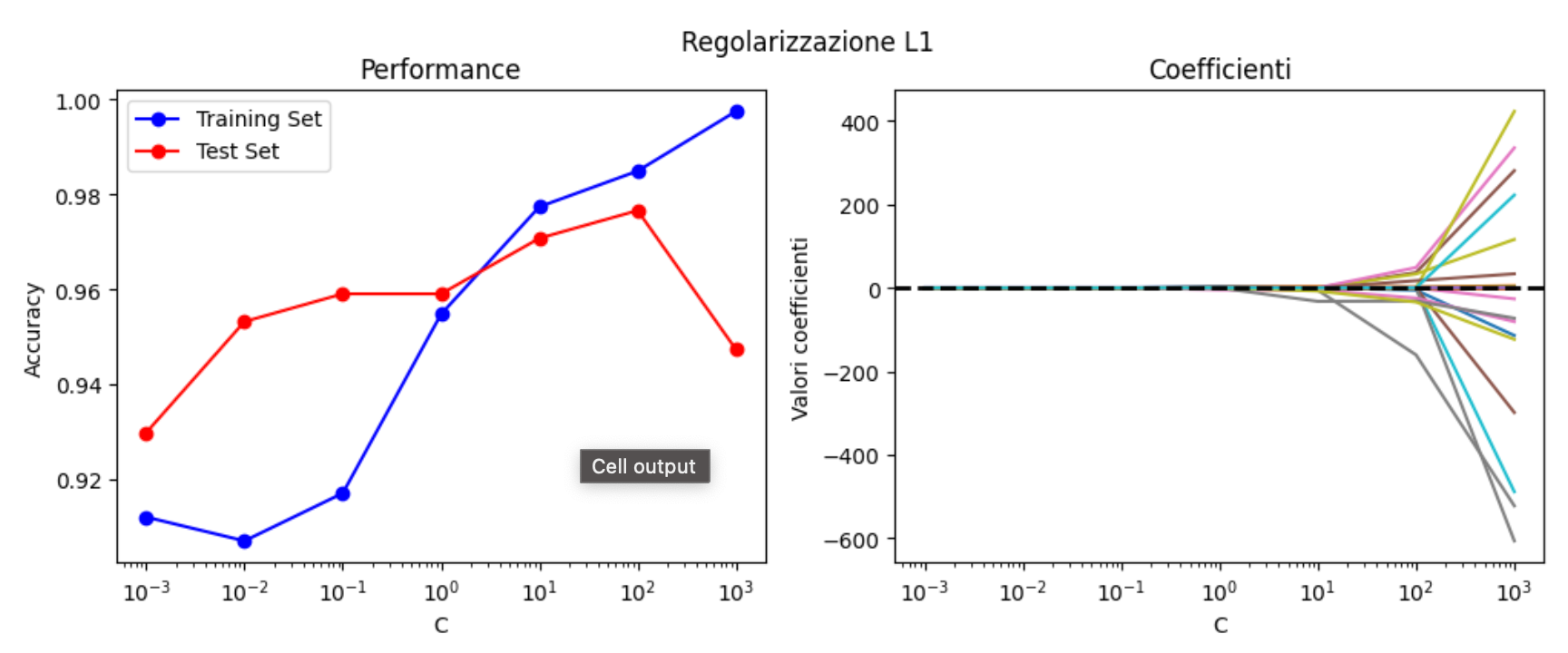
Vediamo come la regolarizzazione L1 appiattisca i coefficienti del modello vicino allo zero per molti livelli di C. I coefficienti con i valori più alti sono, secondo il modello, le feature più importanti ai fini della predizione.
Vediamo anche l'insorgenza dell'overfitting - al valore di \( C = 100 \), la performance del training set aumenta mentre quella nel test set diminuisce.
Applichiamo ora la stessa funzione per valutare gli effetti di L2.
plot_regularization(data, 'l2')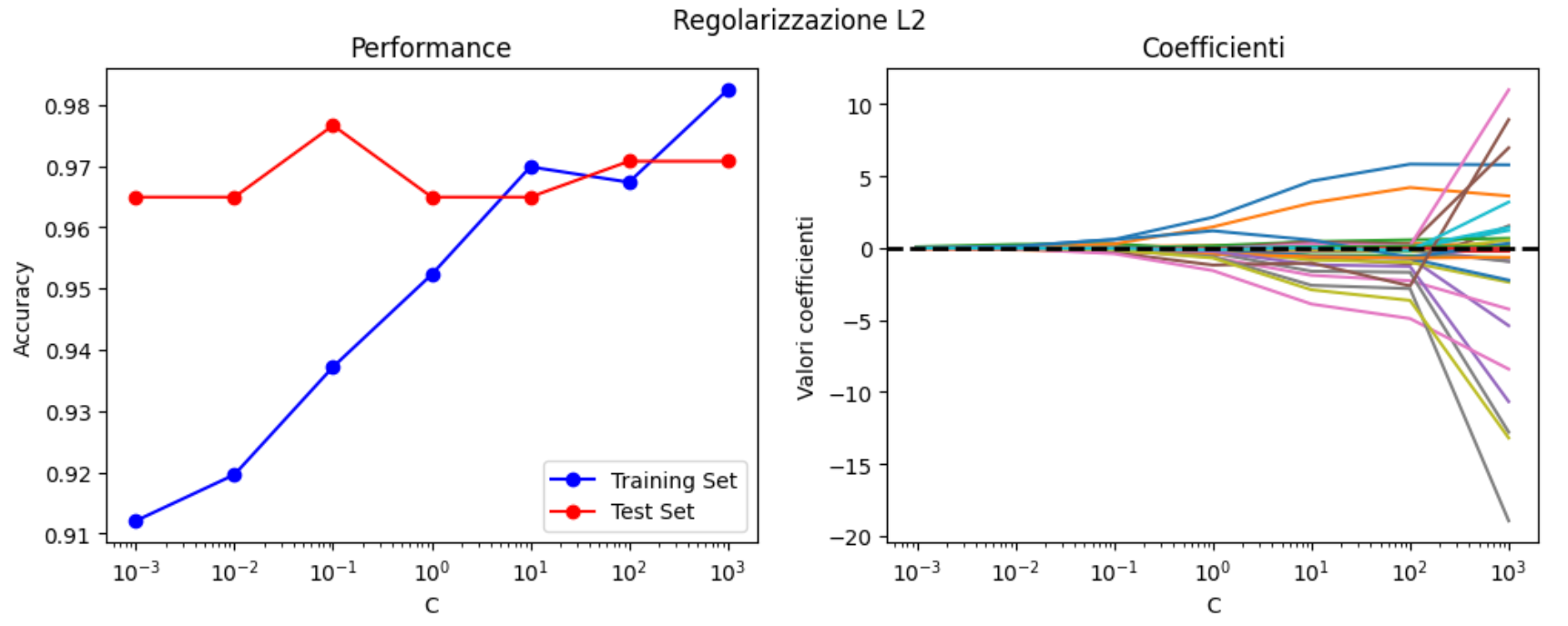
I coefficienti sono sempre sopra lo zero, creando quindi una distribuzione di pesi gradualmente sempre più grandi per le feature più rilevanti. Si nota del leggerissimo overfitting dopo il valore di \( C = 100 \).
Altre tecniche di regolarizzazione
Oltre alle regolarizzazioni L1 e L2, esistono altre tecniche di regolarizzazione che possono essere utilizzate nei modelli di machine learning. Tra queste tecniche troviamo il dropout e l'early stopping.
Dropout
Il dropout è una tecnica utilizzata nelle reti neurali per ridurre l'overfitting. Il dropout funziona spegnendo casualmente alcuni neuroni durante la fase di addestramento, obbligando la rete neurale a trovare modi alternativi per rappresentare i dati.
Early stopping
L'early stopping è un'altra tecnica utilizzata per evitare l'overfitting nei modelli di machine learning. Questa tecnica consiste nel fermare l'addestramento del modello quando la performance sul set di validazione inizia a peggiorare. In questo modo si evita che il modello impari troppo i dati di addestramento e non generalizzi bene sui dati non visti prima.
In generale, l'overfitting può essere evitato utilizzando una combinazione di tecniche di regolarizzazione. Tuttavia, la scelta delle tecniche più appropriate dipenderà dalle caratteristiche del dataset e dal modello di machine learning utilizzato.
Conclusioni
In conclusione, la regolarizzazione è un'importante tecnica di machine learning che aiuta a migliorare le prestazioni dei modelli, evitando l'overfitting sui dati di addestramento.
Le regolarizzazioni L1 e L2 sono le tecniche più utilizzate per questo scopo. L'implementazione di queste tecniche è relativamente semplice in Python grazie alle librerie come scikit-learn e NumPy.
Nel nostro esempio abbiamo visto come la regolarizzazione influisca sulla performance del modello di regressione logistica e come il valore di C influisca sulla regolarizzazione stessa. Abbiamo anche esaminato come i coefficienti dei modelli cambiano al variare del valore di C e come la regolarizzazione L1 e L2 influisce in modo diverso sui coefficienti del modello.







Commenti dalla community