Le reti convolutive vengono utilizzate per processare dati organizzati a griglia come ad esempio immagini e video.

L'operazione di convoluzione è importante perché permette di trovare parti dell'immagine interessanti come ad esempio i contorni degli oggetti di un immagine.

Queste reti godono delle seguenti proprietà:

• Condivisione dei parametri (parameter sharing), implica l'utilizzo dello stesso parametro per più di un unità nella stessa rete
• Interazioni sparse (sparse interactions), ogni input influenza un numero limitato di output e ogni output è influenzato da un numero limitato di input. Solitamente ogni input influenza tutti gli output e tutti gli output sono influenzati da tutti gli input
• Rappresentazioni equivarianti (equivariant representations), l'operazione di convoluzione è invariante per traslazione (conseguenza del parameter sharing).

Il dataset MNIST

Il dataset MNIST è diventato un punto di riferimento standard per l'apprendimento automatico, la classificazione e i sistemi di computer vision.

Questo è stato derivato da un dataset più ampio noto come MNIST Special Database 19, che contiene cifre e lettere minuscole e maiuscole scritte a mano.

Composto da immagini di numeri da 0 a 9 scritti a mano ed è già suddiviso in training set e test set rispettivamente costituiti da 60000 e 10000 elementi.

Passiamo adesso al codice:

import tensorflow as tf 
from keras.datasets import mnist
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from keras.utils import to_categorical
from sklearn.metrics import accuracy_score,f1_score,ConfusionMatrixDisplay,confusion_matrix

(x_train,y_train),(x_test,y_test)=mnist.load_data()

print("Numero di esempi di train:",len(x_train))
print("Numero esempi di test:",len(x_test))
print("Dimensione immagini:",x_train[0].shape)
print("Numero di classi:",len(np.unique(y_train)))

#visualizziamo la prima immagine per ogni classe del train test
for i in range(10):
    index=np.where(y_train==i)[0][0]
    img=x_train[index]
    plt.figure()
    plt.axis("off")
    plt.imshow(img,cmap="gray")

Numero di esempi di train: 60000
Numero esempi di test: 10000
Dimensione immagini: (28, 28)
Numero di classi: 10

Prima di tutto importiamo il MNIST dai dataset presenti sulla libreria keras assegnando i nomi ai nostri train e test.

Successivamente verifichiamo il numero di elementi per il train ed il test, visualizziamo la dimensione delle immagini che dovrebbe essere 28 x 28 ed infine il numero di classi che deve corrispondere a 10 dato che abbiamo numeri da 0 a 9.

Adesso prima di passare allo sviluppo della rete neurale, dobbiamo fare si che i nostri dati siano nel corretto formato affinché tutto possa funzionare in modo appropriato.

La preparazione del dato segue questi step

1. Normalizzazione
2. Reshaping
3. Codifica one-hot della variabile target

Si normalizza il test dividendo ogni pixel per il massimo valore dei pixel stessi, in questo caso il valore massimo sarà 255 perché ci troviamo con una scala di grigi dove lo 0 indica il nero e 255 il bianco.

A questo punto aggiungo una quarta dimensione pari a 1 la quale rappresenta il canale.

Per concludere le etichette di y_train vengono convertite alla codifica one-hot per ottenere un formato categoriale.

#normalizziamo dividendo ogni pixel per il massimo valore dei pixel in questo caso sarà 255 perchè abbiamo una scala di grigi dove 0 è il nero e 255 il bianco
x_train=x_train/x_train.max()
x_test=x_test/x_test.max()


#aggiungo una quarta dimensione pari a 1 che rappresenta il canale. Dato che sono in scala di grigio 
x_train=x_train.reshape(x_train.shape[0],x_train.shape[1],x_train.shape[2],1)
x_test=x_test.reshape(x_test.shape[0],x_test.shape[1],x_test.shape[2],1)

print(x_train.shape)
print(x_test.shape)

#One-hot encoding
y_train_cat=to_categorical(y_train)

(60000, 28, 28, 1)
(10000, 28, 28, 1)

Definizione dell'architettura della rete neurale

Ora i dati sono pronti per essere processati dalla rete neurale. Passiamo alla scrittura del modello usando Keras e TensorFlow, sfruttando l'API funzionale.

Se vuoi saperne di più di Keras, TensorFlow e la sua API di leggere il seguente articolo che introduce agli argomenti menzionati

Introduzione a Tensorflow 2.0 - API e modello sequenziale di deep learning

Tensorflow è il framework creato da Google che permette ai praticanti di machine learning di creare modelli di deep learning ed è spesso la prima soluzione che viene proposta agli analisti che si approcciano per la prima volta al deep learning.

Andrea D’AgostinoDiario Di Un Analista | Data Science, Machine Learning & Analytics

Guardiamo il codice.

# importiamo le librerie essenziali
from keras.models import Sequential
from keras.layers import Dense,Conv2D,Flatten,Dropout,MaxPooling2D
from keras.losses import CategoricalCrossentropy
from keras.optimizers import Adam
from keras.callbacks import EarlyStopping
from tensorflow import keras

K.clear_session()

# definiamo il modello in maniera funzionale
cnn= Sequential()
cnn.add(Conv2D(filters=32, kernel_size=(5,5), padding='same', activation='relu', input_shape=(28, 28, 1)))
cnn.add(MaxPooling2D(strides=2))
cnn.add(Conv2D(filters=48, kernel_size=(5,5), padding='valid', activation='relu'))
cnn.add(MaxPooling2D(strides=2))
cnn.add(Flatten())
cnn.add(Dense(256, activation='relu'))
cnn.add(Dense(84, activation='relu'))
cnn.add(Dense(10, activation='softmax'))

# definizione dell'ottimizzatore
opt=Adam(learning_rate=1e-3) #algoritmo di ottimizzazione, learning rate indica il tasso di apprendimento

# compiliamo il modello prima dell'addestramento
cnn.compile(optimizer=opt,
                   loss='categorical_crossentropy', #loss function
                   metrics=['accuracy'])

print(cnn.summary())

keras.utils.plot_model(cnn, "model.png", show_shapes=True)

La parte finale del codice genera un grafico che riassume l'architettura del modello in questo modo.

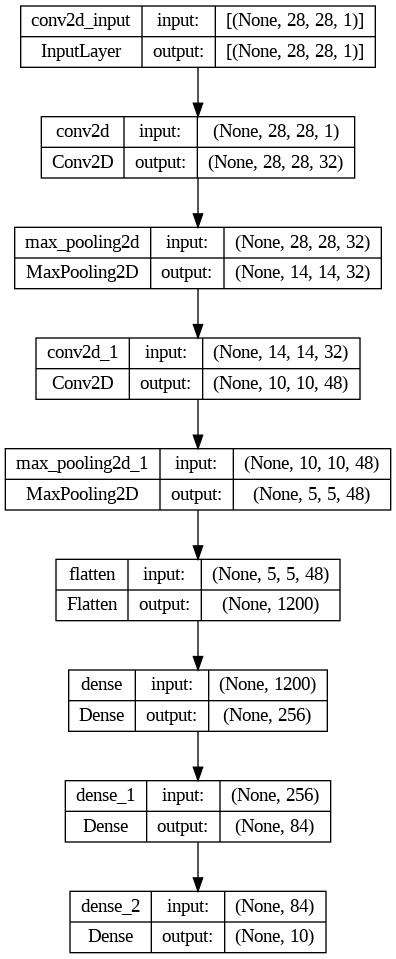
Spieghiamo ora le diverse parti di codice, passo dopo passo.

Primo blocco convolutivo

Questo strato è uno dei blocchi fondamentali di una CNN. Il primo strato convoluzionale ha 32 filtri con un kernel di dimensione 5x5 (può anche essere 3x3).

Il kernel è una matrice di valori che scorre sull'immagine per eseguire l'operazione di convoluzione, ovvero moltiplica i valori dei pixel dell'immagine corrispondenti ai valori del kernel e ne calcola la somma.

Questo processo di convoluzione viene ripetuto in tutta l'immagine per produrre l'output dell'operazione.

La funzione di attivazione non lineare ReLU (Rectified Linear Unit) per l'estrazione delle caratteristiche, se il valore di input è maggiore o uguale a zero, la funzione ReLU restituisce l'input, altrimenti restituisce zero.

Quindi, la funzione ReLU "attiva" l'output solo se l'input è positivo o zero, altrimenti lo "disattiva" impostandolo a zero.

Il parametro padding="same" indica che vengono aggiunti degli zero ai bordi dell'immagine in modo che l'output abbia la stessa dimensione dell'input e rendere possibile l'operazione di convoluzione su ogni posizione dell'input.

MaxPooling2D

Questo strato riduce le dimensioni dell'immagine mantenendo le informazioni più rilevanti, l'operazione viene eseguita selezionando il valore massimo in una finestra di dimensioni predefinite e spostando tale finestra in modo non sovrapposto sull'immagine.

L'argomento strides=2 indica che il max pooling viene applicato con uno spostamento di 2 pixel in orizzontale e verticale.

Secondo blocco convolutivo

Qui viene aggiunto un altro strato convoluzionale con 48 filtri con kernel di dimensione 5x5 e funzione di attivazione ReLU. Il parametro padding="valid" indica che la dimensione dell'output diminuisce ad ogni layer.

Appiattimento (flatten)

Questo strato è utilizzato per appiattire l'output del secondo blocco convolutivo in modo che possa essere collegato ai successivi strati densamente connessi.

Strati densamente connessi

Vengono aggiunti tre strati densamente connessi.

Il primo ha 256 neuroni con attivazione ReLU, seguito da un secondo strato con 84 neuroni con attivazione ReLU.

Infine, l'ultimo strato ha 10 neuroni con attivazione softmax, che è utilizzato per l'output della classificazione in 10 classi (considerando che si tratta di un problema di classificazione con 10 possibili etichette).

Softmax è una funzione di attivazione utilizzata comunemente nell'ultimo strato delle reti neurali per la classificazione multiclasse. Viene utilizzata per convertire gli output numerici di una rete neurale in probabilità, consentendo di ottenere una distribuzione di probabilità su più classi.

Opera su un vettore di numeri reali e restituisce un nuovo vettore in cui ogni elemento è una probabilità compresa tra 0 e 1, e la somma di tutti gli elementi.

Algoritmo di ottimizzazione

Adam, acronimo di "Adaptive Moment Estimation", è un algoritmo di ottimizzazione ampiamente utilizzato per l'addestramento di reti neurali.

È noto per la sua efficacia nel velocizzare la convergenza dell'addestramento e nel superare alcune limitazioni di altri algoritmi di ottimizzazione.

L'idea principale di Adam è combinare concetti di altri due ottimizzatori molto popolari: RMSprop e Momentum.

Questa combinazione rende Adam in grado di adattare il tasso di apprendimento per ogni parametro della rete in base ai gradienti storici e alla varianza dei gradienti.

L'algoritmo Adam è molto popolare nell'addestramento di reti neurali grazie alla sua combinazione di efficienza computazionale, adattabilità del tasso di apprendimento e robustezza rispetto a diverse configurazioni di reti neurali. È spesso il metodo di scelta per l'ottimizzazione in molti problemi di deep learning.

Loss function

La categorical cross entropy è una funzione di costo (loss function) comunemente utilizzata per problemi di classificazione multiclasse, in cui le etichette target sono rappresentate in formato one-hot encoding.

Quando si addestra una rete neurale per una classificazione multiclasse, l'obiettivo è quello di far sì che il modello produca delle probabilità predette per ciascuna classe e si avvicini il più possibile alle etichette target rappresentate in formato one-hot.

La categorical cross entropy misura la discrepanza tra queste probabilità predette e le etichette target, aiutando il modello a imparare ad adattarsi e a produrre predizioni accurate.

Addestramento del modello

Lanciamo l'addestramento con il pezzo di codice qui in basso.

import time

#definiamo callback

keras_callbacks = [
    EarlyStopping(monitor='val_loss', patience=5, verbose=1, min_delta=0.001)#quantità minima di miglioramento richiesta per considerare il valore della perdita come un miglioramento
]
   

start_time = time.time() #registra tempo di inizio
history = cnn.fit(x_train, y_train_cat, epochs=100, batch_size=64, verbose=1,
                    validation_split=0.2, callbacks=keras_callbacks)

end_time = time.time() ##registra tempo di fine

Epoch 1/100
750/750 [==============================] - 87s 113ms/step - loss: 0.1675 - accuracy: 0.9498 - val_loss: 0.0583 - val_accuracy: 0.9811
Epoch 2/100
750/750 [==============================] - 82s 109ms/step - loss: 0.0479 - accuracy: 0.9851 - val_loss: 0.0426 - val_accuracy: 0.9867
Epoch 3/100
750/750 [==============================] - 84s 112ms/step - loss: 0.0325 - accuracy: 0.9901 - val_loss: 0.0410 - val_accuracy: 0.9893
Epoch 4/100
750/750 [==============================] - 81s 108ms/step - loss: 0.0248 - accuracy: 0.9921 - val_loss: 0.0445 - val_accuracy: 0.9874
Epoch 5/100
750/750 [==============================] - 80s 107ms/step - loss: 0.0200 - accuracy: 0.9940 - val_loss: 0.0395 - val_accuracy: 0.9878
Epoch 6/100
750/750 [==============================] - 82s 110ms/step - loss: 0.0151 - accuracy: 0.9951 - val_loss: 0.0576 - val_accuracy: 0.9861
Epoch 7/100
750/750 [==============================] - 80s 106ms/step - loss: 0.0139 - accuracy: 0.9952 - val_loss: 0.0432 - val_accuracy: 0.9899
Epoch 8/100
750/750 [==============================] - 80s 107ms/step - loss: 0.0099 - accuracy: 0.9970 - val_loss: 0.0507 - val_accuracy: 0.9878
Epoch 9/100
750/750 [==============================] - 82s 110ms/step - loss: 0.0106 - accuracy: 0.9965 - val_loss: 0.0470 - val_accuracy: 0.9891
Epoch 10/100
750/750 [==============================] - 81s 108ms/step - loss: 0.0107 - accuracy: 0.9964 - val_loss: 0.0463 - val_accuracy: 0.9892
Epoch 10: early stopping

Grazie alle callback inserite nel fit della CNN possiamo eseguire azioni specifiche durante l'addestramento.

L'EarlyStopping interrompe l'addestramento se il valore della funzione di perdita sulla validazione (val_loss) non migliora per un numero specificato di epoche consecutive (in questo caso ho selezionata una tolleranza di 5 epoche con patience=5), il che significa che l'addestramento si fermerà.

Early Stopping in TensorFlow - impedire l’overfitting di una rete neurale

Come usare una callback per stoppare il training a performance adeguata

Andrea D’AgostinoDiario Di Un Analista | Data Science, Machine Learning & Analytics

Infine, registriamo il tempo di inizio e fine dell'addestramento per calcolarne la durata totale. Questo può essere utile per monitorare quanto tempo impiega il modello a convergere o per confrontare i tempi di addestramento tra diverse configurazioni di modelli.

Creo un dataframe salvando i risultati migliori del modello per: accuracy, validation accuracy, loss, validation loss e tempo. Di seguito ecco i risultati

acc     val_acc    loss     val_loss    computation_time
0.994   0.9878      0.02    0.0395         13.48

Batch size

Il parametro del batch size (dimensione del batch) è un iperparametro importante da considerare durante l'addestramento di una rete neurale.

Indica il numero di campioni di addestramento che vengono passati al modello prima che i gradienti vengano calcolati e i pesi del modello vengano aggiornati.

Il batch size influisce su diversi aspetti dell'addestramento e può avere un impatto sulle prestazioni del modello.

Le dimensioni del batch più comuni sono 64, 128 e 256. Ecco alcune considerazioni generali su ciascuna di queste opzioni:

1. Batch Size 64

Pro: Utilizzare un batch size più piccolo, come 64, può portare a un aggiornamento più frequente dei pesi del modello.
Ciò può essere utile quando si lavora con dataset di grandi dimensioni e risorse computazionali limitate, poiché l'aggiornamento più frequente dei pesi può consentire di utilizzare meno memoria.

Contro: Batch size più piccoli possono rallentare il processo complessivo di addestramento, poiché è necessario calcolare più volte i gradienti e aggiornare i pesi.

2. Batch Size 128

Pro: Un batch size di 128 offre un buon equilibrio tra il vantaggio di aggiornamenti più frequenti dei pesi e un addestramento più veloce rispetto a batch size più piccoli.

Contro: Potrebbe richiedere più memoria rispetto a un batch size di 64, ma solitamente è ancora gestibile con risorse computazionali moderate.

3. Batch Size 256

Pro: Un batch size di 256 può accelerare ulteriormente l'addestramento rispetto a dimensioni del batch più piccole, poiché l'aggiornamento dei pesi avviene ancora meno frequentemente, consentendo di eseguire più calcoli contemporaneamente.

Contro: Potrebbe richiedere più memoria rispetto a batch size più piccoli e potrebbe non essere adatto a tutte le architetture di rete o tipi di dataset.

La scelta della dimensione del batch dipenderà da vari fattori, tra cui la dimensione del dataset, la complessità della rete neurale, le risorse computazionali disponibili e la natura del problema di apprendimento.

Inoltre, è comune eseguire alcuni esperimenti con diverse dimensioni di batch per determinare quale funziona meglio per il tuo specifico caso d'uso.

Risultati

Avendo affrontato il tema della batch size, riportiamo qui una tabella con le varie performance divise proprio per batch size.

       accuracy  val accuracy    loss  val loss  computation_time
64     0.9940        0.9878    0.0200    0.0395             13.58
128    0.9942        0.9898    0.0176    0.0364             14.50
256    0.9951        0.9904    0.0151    0.0362             16.31

Visualizziamo le curve di apprendimento, plottando la loss per le epoche di apprendimento.

val_losses=history.history["val_loss"]
train_losses=history.history["loss"]

epochs = range(1, len(val_losses) + 1)

plt.figure()
plt.title("Training loss")
plt.plot(epochs,val_losses,c="red",label="Validation")
plt.plot(epochs,train_losses,c="orange",label="Training")
plt.xlabel("Epochs")
plt.ylabel("Cross entropy")
plt.legend()

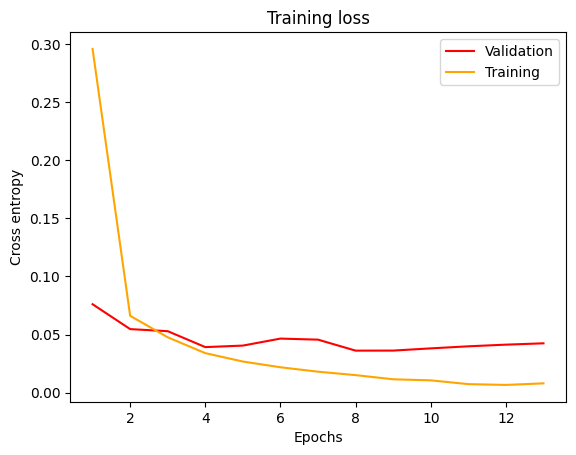
Infine, creiamo una matrice di confusione per mostrare, in formato mappa di calore, le previsioni per ogni classe.

import seaborn as sns

prob=cnn.predict(x_test) 
#Contiene le probabilità di ogni classe predetta per i campioni nel set di #test

y_pred=np.argmax(prob,axis=-1) 
#contiene un array unidimensionale con le etichette predette (indici delle #classi) per ogni campione nel set di test
#La funzione np.argmax() restituisce gli indici dei valori massimi lungo un #asse specificato,
# in questo caso, axis = -1 indica che l'operazione viene eseguita #sull'ultimo asse, cioè l'asse delle classi
#quindi, per ogni campione nel set di test, np.argmax(prob, axis=-1) #restituisce l'indice della classe con la probabilità massima

cm = confusion_matrix(y_test, y_pred)

sns.heatmap(cm, annot=True, fmt='d', cmap='Blues') 
#annot = T aggiunge le etichette dei valori nella mappa di calore, fmt='d' #specifica che i valori devono essere visualizzati come interi, e #cmap='Blues' imposta la scala dei colori come sfumature di blu

plt.xlabel('Predicted')
plt.ylabel('True')
plt.title('Confusion Matrix')
plt.show()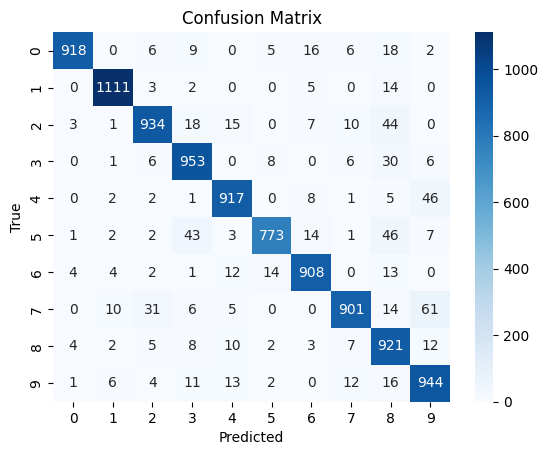

Vediamo come la nostra CNN prevede abbastanza bene e non emergono particolari difficoltà nell'identificare un numero piuttosto che un altro.

Conclusioni

L'utilizzo delle reti neurali convoluzionali (CNN) con il dataset MNIST ha dimostrato di essere una combinazione molto potente per il riconoscimento delle cifre scritte a mano.

Grazie alla loro capacità di apprendere automaticamente le caratteristiche rilevanti dalle immagini, le CNN hanno portato a risultati eccezionali nella classificazione di cifre da 0 a 9.

Durante il percorso di questo articolo, abbiamo esplorato le principali componenti delle reti convoluzionali, compresi i layer di convoluzione, max pooling e le funzioni di attivazione come ReLU e softmax.

Abbiamo visto come queste reti si adattino perfettamente al riconoscimento delle immagini, rivelando un'efficacia sorprendente nel catturare pattern complessi e rappresentare le immagini con elevate capacità discriminative.

Il dataset MNIST si è rivelato un eccellente punto di partenza per apprendere e sperimentare con le CNN. La sua comprensibilità e la sua dimensione relativamente ridotta hanno rappresentato un'opportunità per acquisire familiarità con la progettazione di reti neurali e l'ottimizzazione dei parametri.

Inoltre, abbiamo esplorato l'importanza delle callback nel processo di addestramento del modello, in particolare EarlyStopping che ci ha permesso di evitare l'overfitting e migliorare l'efficienza dell'addestramento.