Introduzione alla PCA in Python con Sklearn, Pandas e Matplotlib

Nel contesto dell'analisi dei dati, ci troviamo spesso ad affrontare sfide complesse dovute alla crescente quantità di informazioni disponibili.

È innegabile che l'accumulo di dati da svariate fonti sia diventato una costante nella nostra vita. Data scientist o meno, tutti praticamente descrivono un fenomeno come una collezione di attributi che lo caratterizzano.

È molto raro lavorare alla risoluzione di una sfida analitica senza dover gestire un insieme di dati multidimensionali - questo è particolarmente evidente oggi, in cui la raccolta di dati è sempre più automatizzata e la tecnologia ci permette di acquisire informazioni da una vasta gamma di fonti, compresi sensori, dispositivi IoT, social media, transazioni online e molto altro.

Per un data scientist, l'obiettivo è comprendere, estrarre significato e ottenere previsioni o insight dai dati stessi: ma solitamente maggiore è la complessità del fenomeno, maggiore sarà la difficoltà di raggiungere questi obiettivi.

Con l'aumentare della complessità dei dati, sorgono nuove sfide. Ecco alcune di queste sfide:

1. Dimensionalità elevata: Avere molte colonne può portare a problemi di dimensionalità elevata, che possono rendere i modelli più complessi e difficili da interpretare. La riduzione della dimensionalità o l'uso di tecniche di selezione delle caratteristiche possono aiutare a mitigare questo problema.
2. Dati rumorosi o sporchi: La raccolta automatica di dati può comportare la presenza di errori, dati mancanti o dati inaffidabili. La pulizia dei dati è una parte critica del processo di analisi.
3. Interpretazione: Con molti attributi, può essere difficile interpretare le relazioni tra di essi e comprendere quali siano le caratteristiche più influenti per un determinato problema.
4. Overfitting: Modelli troppo complessi possono soffrire di overfitting, ossia l'adattamento eccessivo ai dati di addestramento, con conseguente scarsa capacità di generalizzazione ai nuovi dati.
5. Risorse computazionali: L'analisi di dataset grandi e complessi richiede spesso risorse computazionali significative. La scalabilità è una considerazione importante.
6. Privacy e sicurezza: La gestione di dati sensibili o personali richiede attenzione alla privacy e alla sicurezza dei dati.
7. Comunicazione dei risultati: Spiegare le scoperte ottenute da un dataset multidimensionale in modo comprensibile è una sfida importante, soprattutto quando si comunica con stakeholder non tecnici.

Ho scritto un articolo che si collega a questo argomento, che puoi leggere qui 👇

Perché avere un grosso numero di feature può peggiorare il tuo modello

Una attività di feature engineering può essere molto utile per migliorare le performance di un modello predittivo. Questa però può peggiorare i nostri risultati se non teniamo a mente certi principi da evitare.

Diario Di Un Analista | Data Science, Machine Learning & AnalyticsAndrea D’Agostino

In questo articolo, esploreremo come utilizzare la PCA per semplificare e visualizzare dati multidimensionali in modo efficace, rendendo accessibili informazioni complesse multidimensionali.

Intuizione alla base dell'algoritmo PCA

L'analisi dei componenti principali (in inglese Principal Component Analysis, PCA) è una tecnica statistica non supervisionata di decomposizione di dati multidimensionali.

Il suo scopo principale è quello di ridurre in un numero di variabili arbitrarie dette componenti un nostro dataset multidimensionale al fine di

• selezionare feature importanti nel dataset originale
• aumentare il rapporto segnale / rumore
• creare nuove feature da fornire ad un modello di machine learning
• visualizzare dati multidimensionali

In base al numero di componenti che scegliamo, l'algoritmo PCA permette la riduzione del numero di variabili nel dataset originale andando a preservare quelle che spiegano meglio la varianza totale del dataset stesso, andando a combattere la maledizione della dimensionalità (curse of dimensionality).

La maledizione della dimensionalità è un concetto nel machine learning che si riferisce alla difficoltà che si incontra quando si lavora con dati a elevata dimensionalità.

Con l'aumentare del numero di dimensioni, il numero di dati necessari per rappresentare un insieme di dati in modo affidabile aumenta esponenzialmente. Ciò può rendere difficile trovare pattern interessanti nei dati e può causare problemi di overfitting nei modelli di apprendimento automatico.

La trasformazione applicata dalla PCA riduce le dimensioni del dataset creando delle componenti che raccolgono al meglio la varianza dei dati originali. Questo permette di isolare le variabili più rilevanti e di ridurre la complessità del dataset.

La PCA è tipicamente una tecnica difficile da assimilare, soprattutto per studenti e praticanti alle prime armi nel campo della data science e analytics.

La motivazione di questa difficoltà va ricercata nelle basi strettamente matematiche dell'algoritmo.

Ma cosa fa dal punto di vista matematico la PCA?

La PCA permette di proiettare un dataset n-dimensionale in un piano dimensionale più basso.

Sembra complesso, ma in realtà non lo è. Proviamo a intuire il procedimento generale:

quando disegniamo qualcosa su un foglio di carta, stiamo di fatto prendendo una rappresentazione mentale (che possiamo rappresentare in 3 dimensioni) e proiettandola sul foglio, andando a ridurre la qualità e la precisione della rappresentazione.

La rappresentazione su foglio rimane comunque comprensibile e apprezzabile dal prossimo!

Infatti durante l'atto di disegnare andiamo a rappresentare forme, linee e ombreggiature al fine di permettere al prossimo di comprendere quello che noi stiamo pensando nel nostro cervello.

Prendiamo come esempio questa immagine di uno squalo

se volessimo disegnarlo su un foglio di carta, in base al nostro livello di bravura (il mio è molto basso come si può notare), potremmo rappresentarlo così

Il punto che voglio passare è che nonostante la rappresentazione non sia perfettamente 1:1, un osservatore può comprendere facilmente che il disegno rappresenta uno squalo.

Di fatto, l'algoritmo "mentale" che abbiamo usato è simile alla PCA - abbiamo ridotto la dimensionalità, quindi le caratteristiche dello squalo in fotografia, e usato solamente le dimensioni più rilevanti per comunicare il concetto di "squalo" sul foglio di carta.

Matematicamente parlando quindi, non vogliamo solo proiettare il nostro oggetto in un piano dimensionale inferiore, ma vogliamo anche preservare il maggior numero di informazioni rilevanti possibili.

La compressione dei dati

Utilizziamo un semplice dataset per procedere con un esempio. Questo dataset contiene informazioni strutturali su immobili, come grandezza in metri quadri, numero di stanze e così via.

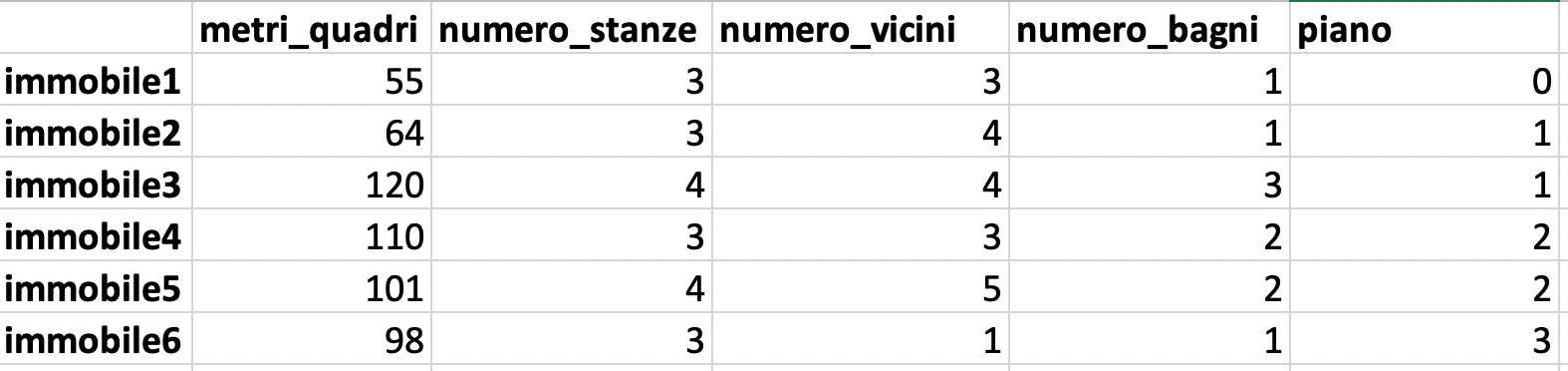
Qui l'obiettivo è mostrare quanto facile è toccare i limiti della visualizzazione dei dati quando si ha un dataset multidimensionale e come la PCA può aiutarci a superare queste limitazioni.

La dimensionalità di un dataset può essere intesa semplicemente come il numero di colonne all'interno dello stesso. Una colonna rappresenta un attributo, una caratteristica, del fenomeno che stiamo studiando. Più dimensioni ci sono, più complesso è il fenomeno.

In questo caso abbiamo un dataset con 5 dimensioni.

Ma che si intende limitazioni della visualizzazione dei dati? Iniziamo a visualizzare i dati partendo da metri_quadri.

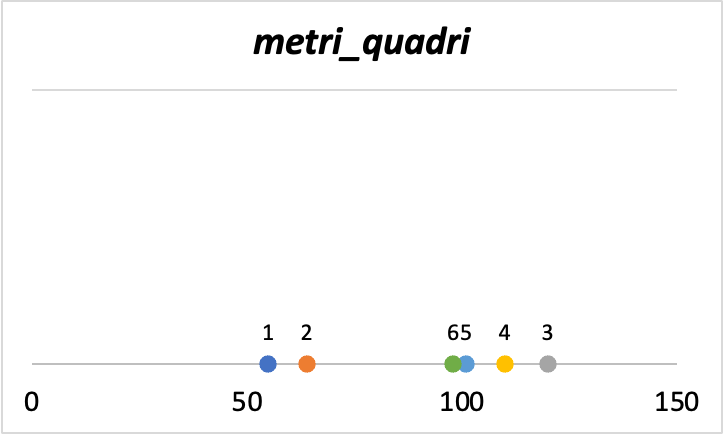
Vediamo come gli immobili 1 e 2 abbiano un basso valore di metri_quadri mentre tutti gli altri sono intorno o superiori al valore di 100. Questo è un grafico uni-dimensionale proprio perché prendiamo in considerazione una sola variabile.

Ora aggiungiamo una dimensione al grafico.

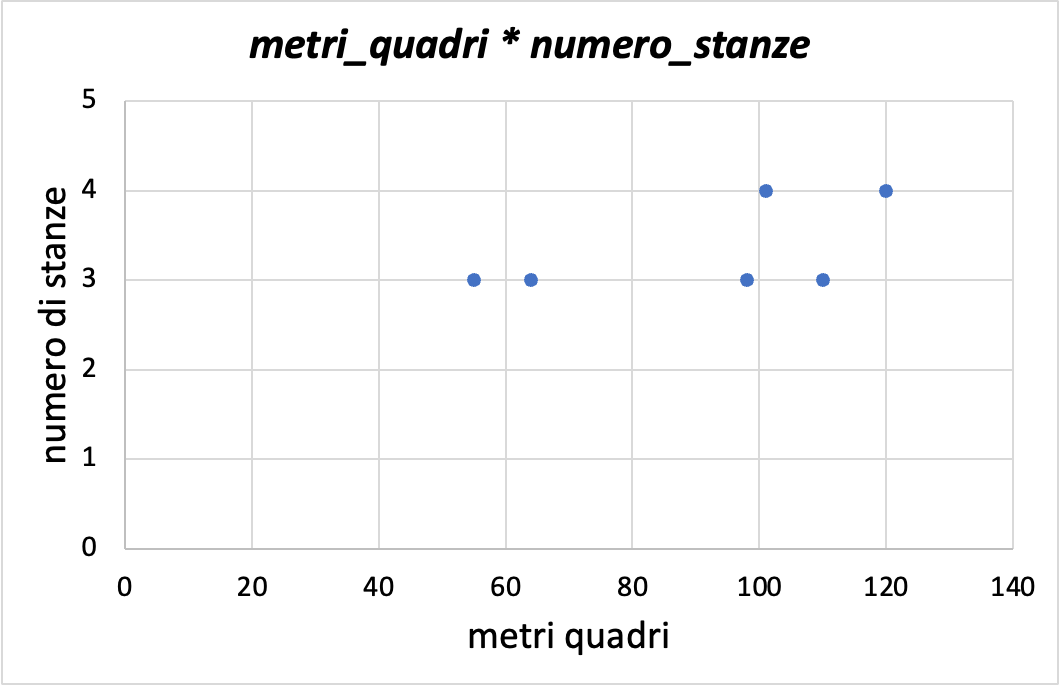
Questo tipo di grafico, chiamato a dispersione (scatterplot in inglese), mostra la relazione tra due variabili. È molto utile per visualizzare correlazioni e interazioni tra variabili.

Questa visualizzazione inizia già ad inserire un buon livello di complessità interpretativa, in quanto richiede una attenta ispezione per comprendere la relazione tra le variabili anche da analisti esperti.

Ora andiamo a inserire ancora un'altra variabile.

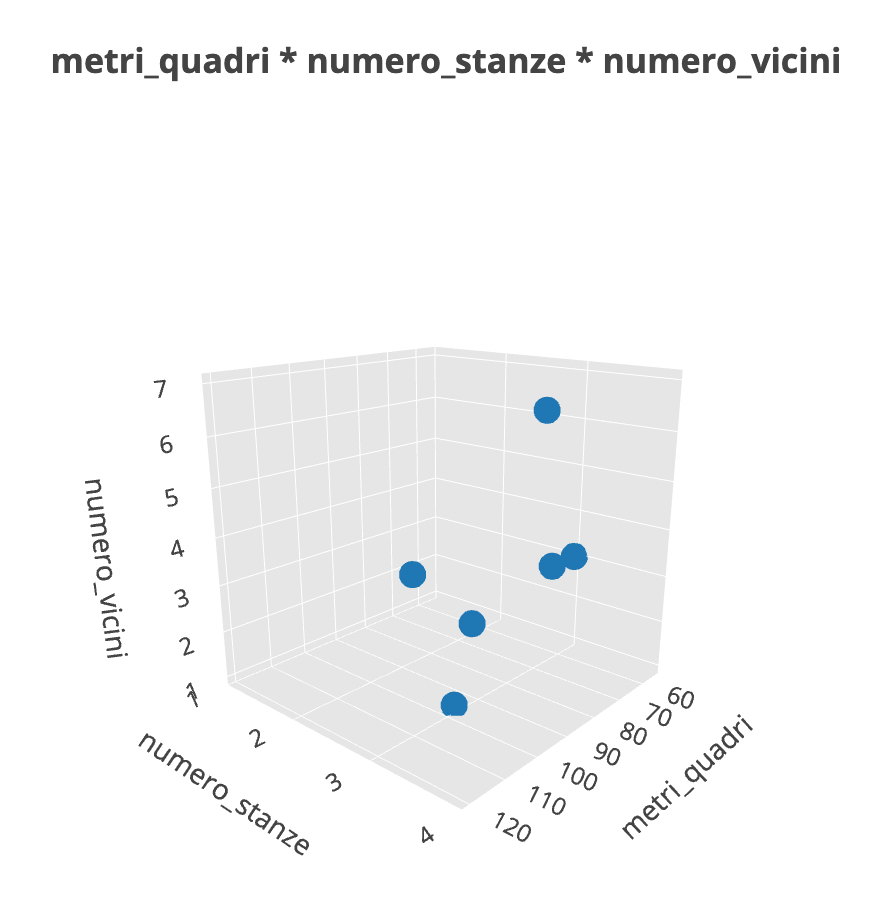
Questa è sicuramente una immagine complessa da elaborare. Dal punto di vista matematico però, questa è una visualizzazione che ha perfettamente senso. Dal punto di vista percettivo e interpretativo, siamo al limite della comprensione umana.

Sappiamo tutti come la nostra interpretazione del mondo si fermi al tridimensionale. Sappiamo anche però che questo dataset è caratterizzato da 5 dimensioni.

Ma quindi come facciamo a visualizzarle tutte?

Non possiamo, a meno che non visualizziamo relazioni bidimensionali tra tutte le variabili, una di fianco all'altra.

Nell'esempio in basso, vediamo come metri_quadri sia messa in relazione bidimensionale con numero_stanze e numero_vicini.

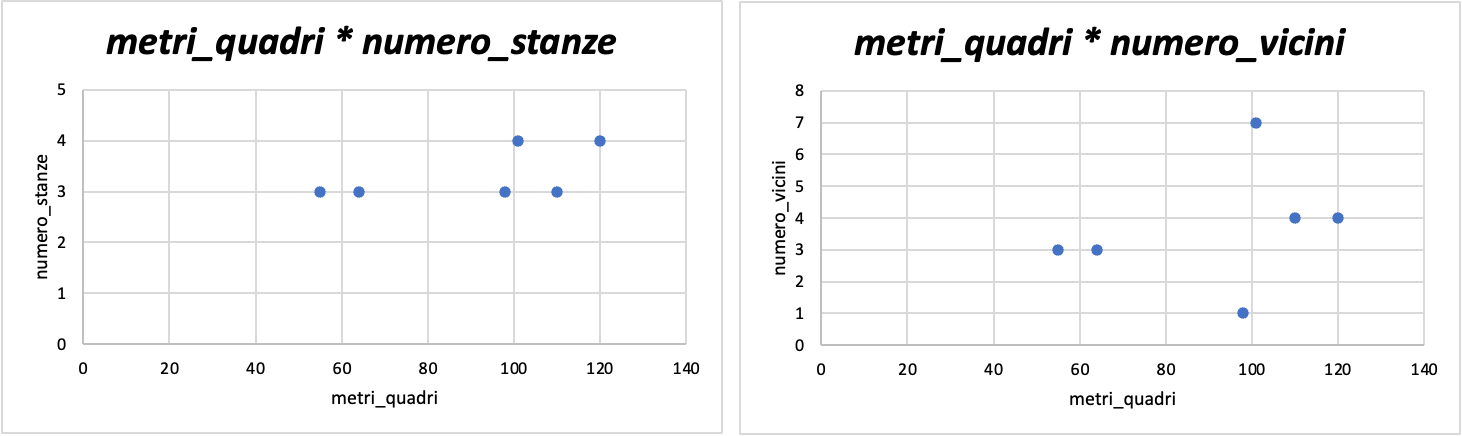
Immaginiamo ora di mettere fianco a fianco tutte le combinazioni possibili...saremmo presto sopraffatti dal grande numero di informazioni da tenere a mente.

Ecco che entra in gioco la PCA. Usando Python (vedremo in seguito), possiamo applicare su questo dataset la classe PCA di Sklearn e ottenere un grafico del genere.

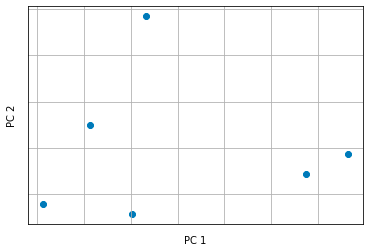
Quello che vediamo qui è un grafico che mostra le componenti principali restituite dalla PCA.

In pratica, l'algoritmo PCA effettua una trasformazione lineare sui dati in modo da trovare la combinazione lineare di feature che meglio spiega la varianza totale del dataset.

Questa combinazione di feature viene chiamata componente principale. Il processo viene ripetuto per ogni componente principale finché non si raggiunge il numero desiderato di componenti.

Il vantaggio di utilizzare la PCA è che permette di ridurre la dimensionalità dei dati mantenendo le informazioni più importanti, eliminando quelle meno rilevanti e rendendo i dati più facili da visualizzare e da utilizzare per costruire modelli di machine learning.

Se ti interessa andare più a fondo sulla matematica dietro la PCA, ti suggerisco le seguenti risorse in inglese:

• PCA Explained Step-By-Step da StatQuest
• Principal Component Analysis (PCA) Explained Visually with Zero Math

Se ti piace apprendere leggendo, ti consiglio questo manuale che copre in dettaglio l'argomento PCA con il focus sul machine learning.

Implementazione in Python

Per applicare la PCA in Python, possiamo utilizzare la libreria scikit-learn, che offre un'implementazione semplice ed efficace.

A questo collegamento è possibile leggere la documentazione della PCA.

Il wine dataset sarà il dataset giocattolo che useremo per l'esempio.

Iniziamo importanto le librerie essenziali

# Importiamo le librerie necessarie
from sklearn.datasets import load_wine
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

# carichiamo il dataset
wine = load_wine()

# convertiamo il dataset in un dataframe Pandas
df = pd.DataFrame(data=wine.data, columns=wine.feature_names)
# creiamo la colonna per il target
df["target"] = wine.target
df
>>>

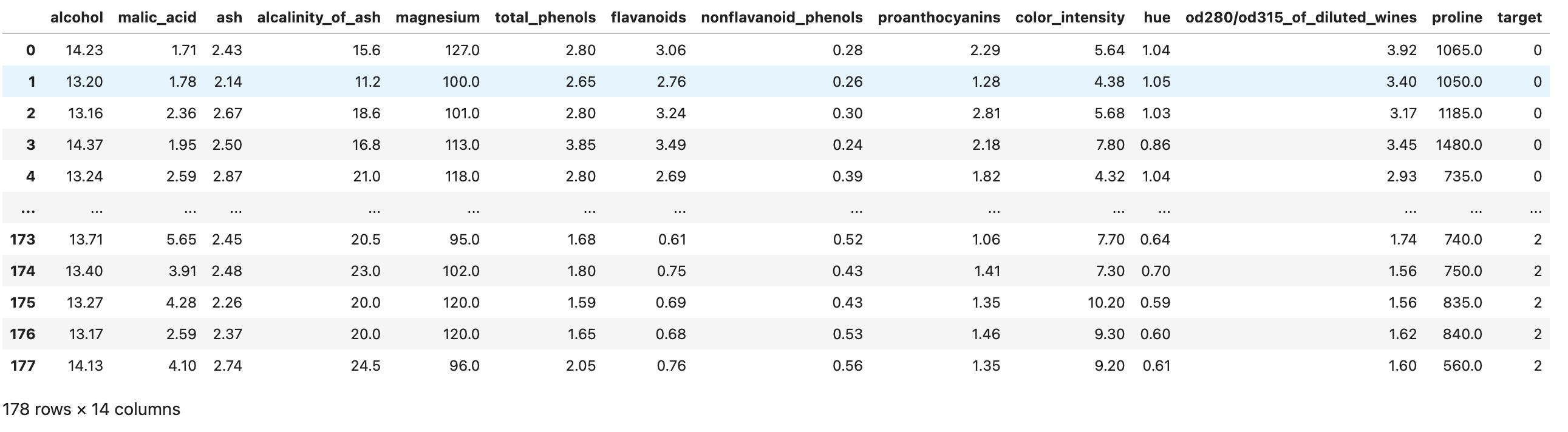
La dimensionalità dei dati è (178, 14) - significa che ci sono 178 righe (esempi da cui un modello di machine learning può apprendere) ognuna di queste descritta da 14 dimensioni.

Applichiamo la normalizzazione dei dati prima di applicare la PCA. È possibile farlo con Sklearn.

# Standardizzare i dati
from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(df.drop(columns=["target"]))

Ora siamo pronti a ridurre le dimensioni. Applichiamo la PCA semplicemente così

# Oggetto PCA specificando il numero di componenti principali desiderate
pca = PCA(n_components=2) # vogliamo proiettare due dimensioni in modo da poterle visualizzare!

# Addestriamo il modello PCA sui dati standardizzati
vecs = pca.fit_transform(X_std)

È possibile specificare qualsiasi numero di dimensioni di output della PCA a patto che queste siano inferiori a 14, cioè il numero totale di dimensioni nel dataset originale.

Ora organizziamo la versione ridotta del dataframe in un nuovo oggetto Pandas Dataframe:

reduced_df = pd.DataFrame(data=vecs, columns=['Principal Component 1', 'Principal Component 2'])
final_df = pd.concat([reduced_df, df[['target']]], axis=1)
final_df
>>>

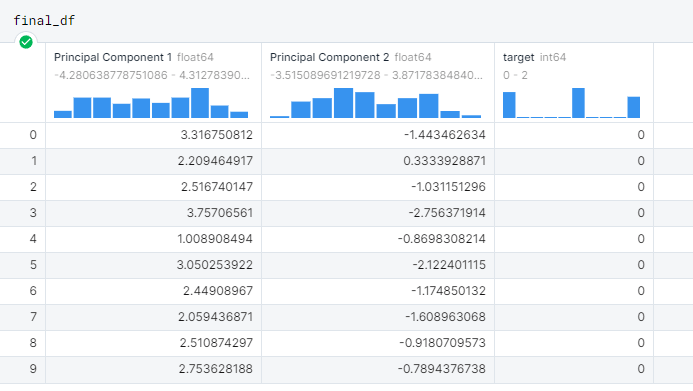
Principal Component 1 e 2 sono le dimensioni di output della PCA, che ora saranno possibili visualizzare con uno scatterplot.

plt.figure(figsize=(8, 6)) # settiamo la grandezza del canvas
targets = list(set(final_df['target'])) # creiamo una lista di possibili target (ne sono 3)
colors = ['r', 'g', 'b'] # definiamo una semplice lista di colori per differenziare i target

# cicliamo per assegnare ogni punto ad un target e colore
for target, color in zip(targets, colors):
    idx = final_df['target'] == target
    plt.scatter(final_df.loc[idx, 'Principal Component 1'], final_df.loc[idx, 'Principal Component 2'], c=color, s=50)

# infine, mostriamo il grafico
plt.legend(targets, title="Target", loc='upper right')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA su Wine Dataset')
plt.show()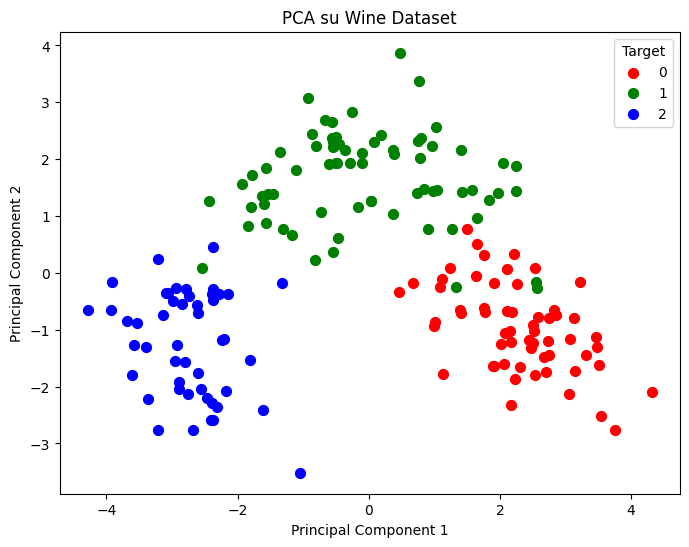

Ed ecco fatto. Questo grafico mostra la differenza tra i vini descritta dalle 14 variabili iniziali, ma ridotte a 2 dalla PCA. La PCA ha ritenuto le informazioni più rilevanti e nel mentre ridotto il rumore presente nel dataset.

Ecco l'intero codice per applicare la PCA con Sklearn, Pandas e Matplotlib in Python.

import pandas as pd
from sklearn.decomposition import PCA
import matplotlib.pyplot as plt

wine = load_wine()

df = pd.DataFrame(data=wine.data, columns=wine.feature_names)

df["target"] = wine.target

from sklearn.preprocessing import StandardScaler
X_std = StandardScaler().fit_transform(df.drop(columns=["target"]))

pca = PCA(n_components=2)

vecs = pca.fit_transform(X_std)

reduced_df = pd.DataFrame(data=vecs, columns=['Principal Component 1', 'Principal Component 2'])
final_df = pd.concat([reduced_df, df[['target']]], axis=1)

plt.figure(figsize=(8, 6))
targets = list(set(final_df['target']))
colors = ['r', 'g', 'b']

for target, color in zip(targets, colors):
    idx = final_df['target'] == target
    plt.scatter(final_df.loc[idx, 'Principal Component 1'], final_df.loc[idx, 'Principal Component 2'], c=color, s=50)

plt.legend(targets, title="Target", loc='upper right')
plt.xlabel('Principal Component 1')
plt.ylabel('Principal Component 2')
plt.title('PCA su Wine Dataset')
plt.show()

Casi d'uso della PCA

Di seguito una lista dei casi d'uso più comuni della PCA in ambito data science.

Migliorare le velocità di addestramento di modelli di machine learning

I dati compressi dalla PCA forniscono le informazioni importanti e sono molto più digeribili da un modello di machine learning, che ora basa il suo apprendimento su un numero di feature ridotto invece che sulla totalità delle feature presenti nel dataset originale.

Selezione delle feature

La PCA è essenzialmente uno strumento di selezione delle feature. Quando andiamo ad applicarla, cerchiamo le feature che spiegano la varianza del dataset al meglio.

È possibile creare una classifica delle componenti principali e ordinarle per importanza, con il primo componente che spiega la maggior varianza e l'ultimo componente che spiega il minimo.

Analizzando le componenti principali è possibile risalire alle feature originali e escludere quelle che non contribuiscono a preservare l'informazione nel piano dimensionale ridotto creato dalla PCA.

Identificazione delle anomalie

La PCA viene spesso utilizzato nell'identificazione delle anomalie perché può aiutare a identificare pattern nei dati che non sono facilmente distinguibili ad occhio nudo.

Le anomalie spesso appaiono come punti dati lontani dal gruppo principale nello spazio dimensionale inferiore, rendendoli più facili da rilevare.

Identificazione del segnale

In contrapposizione all'identificazione delle anomalie, la PCA è molto utile anche per la signal detection (identificazione del segnale).

Infatti, come la PCA può mettere in risalto le anomalie, può anche rimuovere il "rumore di fondo" che non contribuisce alla variabilità totale dei dati. Nel contesto del riconoscimento vocale, questo permette all'utilizzatore di isolare meglio le tracce vocali e di migliorare i sistemi di identificazione della persona attraverso voce.

Compressione delle immagini

Lavorare con le immagini può essere oneroso se abbiamo vincoli particolari, come quello di salvare l'immagine in un certo formato. Senza andare nel dettaglio, la PCA può essere utile per comprimere le immagini mantenendo comunque le informazioni presenti in esse.

Questo permette a algoritmi di machine learning di addestrarsi più velocemente a discapito di informazioni compresse ma di una certa qualità.

Conclusioni

Grazie per la tua attenzione 🙏Spero che la lettura sia stata piacevole e che tu abbia imparato qualcosa di nuovo.

Ricapitolando,

• hai appreso cosa significa dimensionalità di un dataset e le complicazioni che ne derivano
• hai imparato come funziona intuitivamente l'algoritmo PCA passo dopo passo
• hai imparato come implementarla in Python con Sklearn
• e infine hai appreso quali siano i casi d'uso più comuni della PCA in ambito data science

Se hai trovato questo articolo utile condividilo con i tuoi amici o colleghi appassionati e condividi il tuo feedback!

Alla prossima,

Andrea