Come creare indicatori POSET in Python

Gli indici sintetici aggregati sono strumenti ampiamente usati per riassumere molteplici indicatori in un unico valore numerico.

Vengono utilizzati in svariati ambiti: dalla valutazione delle performance aziendali, alla qualità della vita nelle città, fino all’efficienza dei sistemi sanitari. L’obiettivo è fornire una misura semplice, interpretabile e comparabile. Tuttavia, l’apparente semplicità di questi indici spesso maschera decisioni arbitrarie, perdita di informazione, e distorsioni nelle gerarchie risultanti.

Uno dei principali problemi è legato alla scelta dei pesi: attribuire un peso maggiore a un indicatore rispetto a un altro implica una preferenza soggettiva. Inoltre, la sintesi in un unico numero forza un ordinamento totale, anche tra unità che differiscono su più dimensioni in modo non confrontabile, forzare un ordinamento lineare attraverso un punteggio unico porta a semplificazioni eccessive e conclusioni potenzialmente fuorvianti.

A fronte di questi limiti, esistono approcci alternativi. Tra questi, i POSET (Partially Ordered Sets, insiemi parzialmente ordinati) offrono un modo più fedele di rappresentare la complessità dei dati multidimensionali.

Invece di sintetizzare tutte le informazioni in un numero, i POSET si basano su una relazione di dominanza parziale: un’unità domina un’altra se è migliore su tutte le dimensioni considerate. Quando ciò non accade, le due unità rimangono incomparabili.

L’approccio POSET consente quindi di rappresentare la struttura gerarchica implicita nei dati senza forzare confronti dove non sono logicamente giustificabili. Questo lo rende particolarmente utile in contesti decisionali trasparenti, dove la coerenza metodologica è preferibile alla semplificazione forzata.

Partendo dai fondamenti teorici, costruiremo un esempio pratico con un dataset reale (Wine Quality) e discuteremo l’interpretazione dei risultati. Vedremo che, in presenza di dimensioni conflittuali, i POSET rappresentano un compromesso robusto e interpretabile, preservando l’informazione originale senza imporre un ordinamento arbitrario.

Fondamenti teorici

Per comprendere l’approccio POSET è necessario partire da alcuni concetti fondamentali della teoria degli insiemi e dell’ordinamento. A differenza dei metodi aggregativi, che producono un ordinamento totale e forzato tra le unità, il POSET si fonda sulla relazione di dominanza parziale, che permette di riconoscere anche l’incomparabilità tra elementi.

Cosa è un insieme parzialmente ordinato?

Un insieme parzialmente ordinato (in inglese Partially Ordered Set, da cui l’acronimo POSET) è una coppia \( (P, \leq) \), dove:

• \( \text{P} \) è un insieme non vuoto di elementi (es. paesi, aziende, individui, prodotti),
• \( \leq \) è una relazione binaria su \( \text{P} \) che gode di tre proprietà:
  1. Riflessività (ogni elemento è in relazione con sé stesso):
     \[ \forall x \in P,\quad x \leq x \]
  2. Antisimmetria, (se due elementi sono in relazione tra loro in entrambe le direzioni, allora sono uguali):
     \[ \forall x, y \in P,\quad (x \leq y \land y \leq x) \Rightarrow x = y \]
  3. Transitività (se un elemento è in relazione con un secondo, e il secondo con un terzo, allora il primo è in relazione con il terzo):
     \[ \forall x, y, z \in P,\quad (x \leq y \land y \leq z) \Rightarrow x \leq z \]

In termini pratici, si dice che un elemento \( \text{x} \) domina un elemento \( \text{y} \) (cioè \( x \leq y) \) se è migliore o uguale in tutte le dimensioni rilevanti, e strettamente migliore in almeno una.

Questa struttura si contrappone a un ordinamento totale, in cui ogni coppia di elementi è confrontabile (cioè per ogni \( \text{x} \), \( \text{y} \) vale \( x \leq y \) oppure \( y \leq x \)). L’ordinamento parziale invece ammette che alcune coppie siano incomparabili, e questa è una delle sue forze analitiche.

Relazione di dominanza parziale

Nel contesto multi-indicatore, l’ordinamento parziale si costruisce introducendo una relazione di dominanza tra vettori. Dati due oggetti \( a=(a_1, a_2, ..., a_n) \) e \( b=(b_1, b_2, ..., b_n) \), diciamo che \( a \leq b \) (cioè \( \text{a} \) domina \( \text{b} \)) se:

• per ogni \( \text{i}, a_i \leq b_i \)​ (ovvero \( \text{a} \) non è peggiore in nessuna dimensione),
• e per almeno un \( \text{j}, a_j \leq b_j \)​ (ovvero \( \text{a} \) è strettamente migliore in almeno una).

Questa relazione costruisce una matrice di dominanza che rappresenta chi domina chi nel dataset. Se due oggetti non soddisfano i criteri reciproci di dominanza, risultano incomparabili.

Ad esempio:

• Se \( A=(7, 5, 6) \) e \( B=(8, 5, 7) \), allora \( A \leq BA \) (perché \( \text{B} \) è almeno pari in ogni dimensione e strettamente migliore in due),
• Se \( C=(7, 6, 8) \) e \( D=(6, 7, 7) \), allora \( \text{C} \) e \( \text{D} \) sono incomparabili, perché ognuno è migliore in almeno una dimensione, ma peggiore in un’altra.

Questa incomparabilità esplicita è una caratteristica chiave dei POSET: essa preserva l’informazione originale senza forzare ranking artificiali. In molte applicazioni reali, come la valutazione di qualità del vino, di città, o di ospedali, l’incomparabilità non è un errore, ma una rappresentazione fedele della complessità.

Come costruire un indice POSET

Nel nostro esempio utilizziamo il dataset winequality-red.csv, che contiene 1599 vini rossi, ciascuno descritto da 11 variabili chimico-fisiche e da un punteggio di qualità (quality).

Puoi scaricare il dataset qui:

Wine Quality Dataset

Wine Quality Prediction - Classification Prediction

Kaggle

Le variabili disponibili sono:

• fixed acidity: acido tartarico (g/dm³)
• volatile acidity: acido acetico (g/dm³)
• citric acid: (g/dm³)
• residual sugar: zuccheri residui (g/dm³)
• chlorides: cloruri (g/dm³)
• free sulfur dioxide: SO₂ libero (mg/dm³)
• total sulfur dioxide: SO₂ totale (mg/dm³)
• density: densità (g/cm³)
• pH: acidità
• sulphates: solfati (g/dm³)
• alcohol: titolo alcolometrico (% vol.)

Una scelta razionale può includere:

• alcohol (positivo)
• volatile acidity (negativo)
• sulphates (positivo)
• residual sugar (positivo fino a un certo punto, poi neutro)
• citric acid (positivo)

Per POSET, è importante standardizzare la direzione semantica: se una variabile ha effetto negativo, va trasformata (es. -volatile_acidity) prima di valutare la dominanza.

Costruzione della matrice di dominanza

Per costruire la relazione di dominanza parziale tra le osservazioni (i vini), si procede come segue:

• Si selezionano n osservazioni dal dataset (ad es. un sottoinsieme di 20 vini per motivi di leggibilità).
• Ogni vino è rappresentato da un vettore di m indicatori.
• L’osservazione \( \text{A} \) domina \( \text{B} \) se ogni indicatore in \( \text{A} \) è maggiore o uguale al corrispondente in \( \text{B} \), e almeno uno è strettamente maggiore.

Esempio pratico in Python

In questa sezione mostriamo passo dopo passo come costruire un ordinamento parziale (POSET) utilizzando Python. Useremo un sottoinsieme del dataset Wine fornito dalla libreria sklearn.datasets, che contiene caratteristiche chimiche di diversi vini e un punteggio di qualità.

Caricamento e preparazione dei dati

Utilizziamo pandas per gestire il dataset, numpy per le operazioni numeriche e networkx per costruire e visualizzare il diagramma di Hasse.

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import networkx as nx
from sklearn.datasets import load_wine
from sklearn.preprocessing import MinMaxScaler

# Caricamento del dataset wine
data = load_wine()
df = pd.DataFrame(data.data, columns=data.feature_names)
df['target'] = data.target  # varietà di vino

# Scegliamo un sottoinsieme di 3 variabili quantitative
features = ['alcohol', 'malic_acid', 'color_intensity']
df_subset = df[features].copy()

# Normalizzazione min-max per comparabilità
scaler = MinMaxScaler()
df_norm = pd.DataFrame(scaler.fit_transform(df_subset), columns=features)

# Aggiungiamo un ID per riferimento nei grafi
df_norm['ID'] = df_norm.index

Ogni riga del dataset rappresenta un vino, descritto da 3 caratteristiche numeriche. Diciamo che:

• Un vino A domina B se ha valori maggiori o uguali in tutte le dimensioni, e strettamente maggiori in almeno una.

Questo è proprio un ordinamento parziale: non puoi sempre dire se un vino è "migliore" di un altro, perché magari uno ha più alcol ma meno intensità di colore.

Matrice di dominanza

Due osservazioni \( \text{A} \) e \( \text{B} \) sono comparabili se \( \text{A} \) domina \( \text{B} \) in tutte le dimensioni considerate (cioè, \( \text{A} \) è maggiore o uguale a \( \text{B} \) in tutte le variabili, e strettamente maggiore in almeno una).

Costruiamo la matrice di dominanza D, dove D[i][j] = 1 se il punto i domina j.

def is_dominant(a, b):
    """Restituisce True se a domina b."""
    return np.all(a >= b) and np.any(a > b)

# Costruzione della matrice di dominanza
n = len(df_norm)
D = np.zeros((n, n), dtype=int)

for i in range(n):
    for j in range(n):
        if i != j:
            if is_dominant(df_norm.loc[i, features].values, df_norm.loc[j, features].values):
                D[i, j] = 1

# Convertiamo in DataFrame per ispezione
dominance_df = pd.DataFrame(D, index=df_norm['ID'], columns=df_norm['ID'])
print("Matrice di dominanza (estratto):")
print(dominance_df.iloc[:10, :10])


>>>
Matrice di dominanza (estratto):
ID  0  1  2  3  4  5  6  7  8  9
ID                              
0   0  0  0  0  0  0  0  0  0  0
1   0  0  0  0  0  0  0  0  0  0
2   0  0  0  0  0  0  0  0  0  0
3   1  1  0  0  0  1  0  0  0  1
4   0  0  0  0  0  0  0  0  0  0
5   0  0  0  0  0  0  0  0  0  0
6   0  1  0  0  0  0  0  0  0  0
7   0  1  0  0  0  0  0  0  0  0
8   0  0  0  0  0  0  0  0  0  0
9   0  0  0  0  0  0  0  0  0  0

La matrice di dominanza appena calcolata dice, per ogni coppia \( \text{i, j} \):

• 1 se \( \text{i} \) domina \( \text{j} \)
• 0 altrimenti

Per esempio, nella riga 3, trovi valori 1 nelle colonne 0, 1, 5, 9. Questo vuol dire: l'elemento 3 domina gli elementi 0, 1, 5, 9.

Costruzione del diagramma di Hasse

Rappresentiamo le relazioni di dominanza con un grafo orientato aciclico. Riduciamo le relazioni transitivamente per ottenere il diagramma di Hasse, che mostra solo le dominanze dirette.

def transitive_reduction(D):
    """Rimuove gli archi transitivi dalla matrice di dominanza."""
    G = nx.DiGraph()
    for i in range(len(D)):
        for j in range(len(D)):
            if D[i, j]:
                G.add_edge(i, j)

    # Riduzione transitiva
    G_reduced = nx.transitive_reduction(G)
    return G_reduced

# Costruzione grafo
G = transitive_reduction(D)

# Visualizzazione
plt.figure(figsize=(12, 10))
pos = nx.spring_layout(G, seed=42)
nx.draw(G, pos, with_labels=True, node_size=500, node_color='lightblue', arrowsize=15)
plt.title("Diagramma di Hasse - Ordinamento parziale su vini")
plt.show()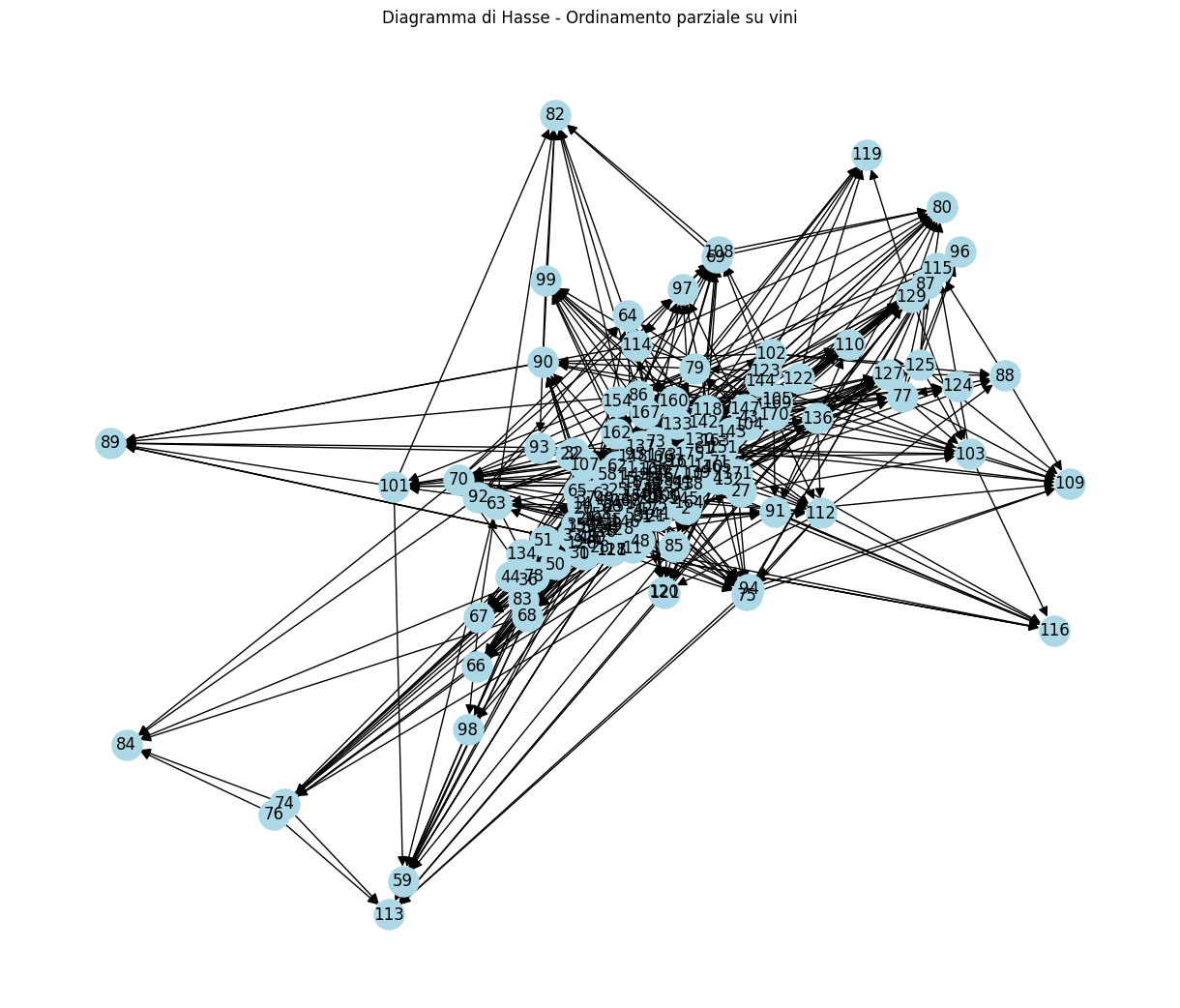

Analisi dell’incomparabilità

Vediamo ora quanti elementi sono incomparabili tra loro. Due unità i e j sono incomparabili se nessuna domina l’altra.

incomparable_pairs = []
for i in range(n):
    for j in range(i + 1, n):
        if D[i, j] == 0 and D[j, i] == 0:
            incomparable_pairs.append((i, j))

print(f"Numero di coppie incomparabili: {len(incomparable_pairs)}")
print("Esempi di coppie incomparabili (max 10):")
print(incomparable_pairs[:10])

>>>
Numero di coppie incomparabili: 8920
Esempi di coppie incomparabili (max 10):
[(0, 1), (0, 2), (0, 4), (0, 5), (0, 6), (0, 7), (0, 8), (0, 9), (0, 10), (0, 12)]

Diventa un professionista dei dati con il corso di Google

Google Data Analytics Certificate

Un programma professionale online, creato da Google, per imparare ad analizzare i dati con strumenti come Excel, SQL, R e Tableau. Non serve esperienza pregressa. Ideale per entrare nel mondo del lavoro data-driven.

Inizia il corso su Coursera

Confronto con un ordinamento sintetico tradizionale

Se usassimo un indice aggregato, otterremmo un ordinamento totale forzato. Usiamo la media normalizzata per ciascun vino come esempio:

# Calcolo indice sintetico (media delle 3 variabili)
df_norm['aggregated_index'] = df_norm[features].mean(axis=1)

# Ordinamento totale
df_ordered = df_norm.sort_values(by='aggregated_index', ascending=False)
print("Top 5 vini secondo indice aggregato:")
print(df_ordered[['aggregated_index'] + features].head(5))

>>>
Top 5 vini secondo indice aggregato:
     aggregated_index   alcohol  malic_acid  color_intensity
173          0.741133  0.705263    0.970356         0.547782
177          0.718530  0.815789    0.664032         0.675768
156          0.689005  0.739474    0.667984         0.659556
158          0.685608  0.871053    0.185771         1.000000
175          0.683390  0.589474    0.699605         0.761092

Questo esempio mostra la differenza concettuale e pratica tra POSET e ranking sintetico. Con l’indice aggregato, ogni unità è forzatamente ordinata; con POSET, si mantengono le relazioni logiche di dominanza, senza introdurre arbitrarietà o perdita informativa. L’uso di grafi orientati consente anche una visualizzazione chiara della gerarchia parziale e dell’incomparabilità tra unità.

Interpretazione dei risultati

Uno degli aspetti più interessanti dell’approccio POSET è che non tutte le unità sono confrontabili. A differenza di un ordinamento totale, dove ogni elemento ha una posizione univoca, l’ordinamento parziale preserva l’informazione strutturale dei dati: alcune unità dominano, altre sono dominate, molte sono incomparabili. Questo ha implicazioni importanti in termini di interpretabilità e decision making.

Nel contesto dell’esempio con i vini, l’assenza di un ordinamento completo implica che alcuni vini sono migliori su certe dimensioni e peggiori su altre. Ad esempio, un vino potrebbe avere un alto contenuto di alcol ma una bassa intensità di colore, mentre un altro vino presenta l’opposto. In questi casi, non esiste una dominanza netta, e i due vini risultano incomparabili.

Dal punto di vista decisionale, questa informazione è preziosa: forzare un ranking totale maschera questi trade-off e può portare a scelte subottimali.

Verifichiamo nel codice quanti nodi sono massimali, cioè non dominati da nessun altro, e quanti sono minimali, cioè non dominano nessun altro:

# Estraiamo i nodi massimali (nessun successore nel grafo)
maximal_nodes = [node for node in G.nodes if G.out_degree(node) == 0]

# Estraiamo i nodi minimali (nessun predecessore)
minimal_nodes = [node for node in G.nodes if G.in_degree(node) == 0]

print(f"Numero di vini massimali (non dominati): {len(maximal_nodes)}")
print(f"Numero di vini minimali (dominati da tutti o incomparabili): {len(minimal_nodes)}")

>>>
Numero di vini massimali (non dominati): 10
Numero di vini minimali (dominati da tutti o incomparabili): 22

L’alto numero di nodi massimali suggerisce che esistono molte alternative valide senza una chiara gerarchia. Questo riflette bene la realtà dei sistemi multi-criterio, dove non sempre esiste una “scelta migliore” universalmente valida.

Cluster di vini non confrontabili

Possiamo identificare gruppi di vini che non sono confrontabili tra loro. Si tratta di sottografi in cui i nodi non sono collegati da alcuna relazione di dominanza. Usiamo networkx per identificare le componenti connesse nel grafo non orientato associato:

# Convertiamo il grafo orientato in non orientato
G_undirected = G.to_undirected()

# Troviamo i cluster di nodi non confrontabili (componenti connesse)
components = list(nx.connected_components(G_undirected))

# Filtriamo solo i cluster con almeno 3 elementi
clusters = [c for c in components if len(c) >= 3]

print(f"Numero di cluster di vini non confrontabili (≥3 unità): {len(clusters)}")
print("Esempio di cluster (fino a 3):")
for c in clusters[:3]:
    print(sorted(c))

>>>
Numero di cluster di vini non confrontabili (≥3 unità): 1
Esempio di cluster (fino a 3):
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125, 126, 127, 128, 129, 130, 131, 132, 133, 134, 135, 136, 137, 138, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 152, 153, 154, 155, 156, 157, 158, 159, 160, 161, 162, 163, 164, 165, 166, 167, 168, 169, 170, 171, 172, 173, 174, 175, 176, 177]

Questi gruppi rappresentano regioni dello spazio multidimensionale in cui le unità sono equivalenti in termini di dominanza: non c’è un modo oggettivo per affermare che un vino sia “meglio” dell’altro, a meno di introdurre un criterio esterno.

Diagramma di Hasse con focus sui massimali

Per visualizzare meglio la struttura dell’ordinamento, possiamo evidenziare i nodi massimali (scelte ottime) nel diagramma di Hasse:

# Colore blu per i nodi massimali, grigio per gli altri
node_colors = ['skyblue' if node in maximal_nodes else 'lightgrey' for node in G.nodes]

plt.figure(figsize=(12, 10))
pos = nx.spring_layout(G, seed=42)
nx.draw(G, pos, with_labels=True, node_size=600, node_color=node_colors, arrowsize=15)
plt.title("Nodi massimali evidenziati (non dominati)")
plt.show()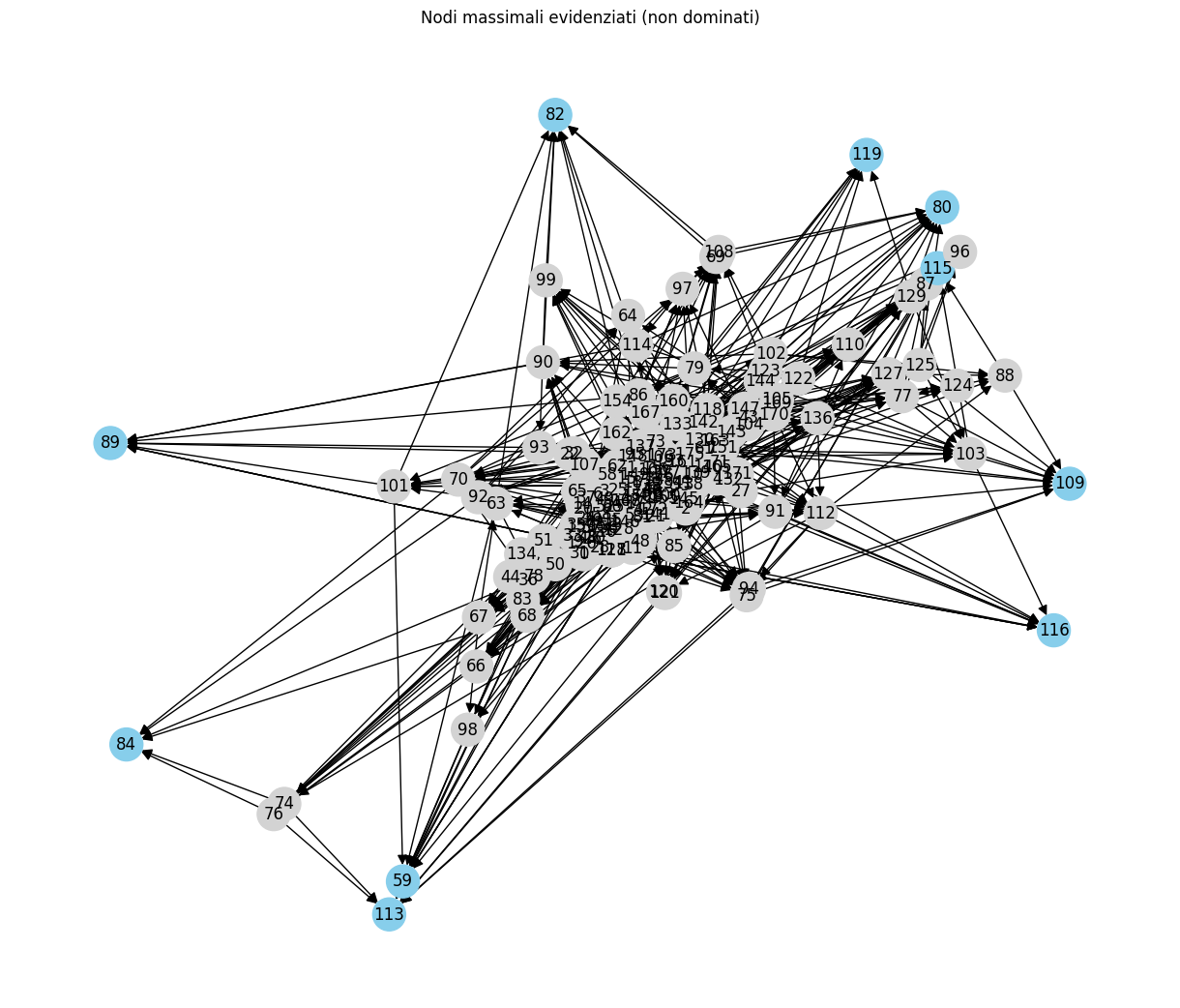

In scenari reali, questi nodi massimali corrisponderebbero a soluzioni non dominate, ovvero le opzioni migliori in un’ottica di Pareto-efficienza. Il decision maker potrebbe scegliere uno di questi in base a preferenze personali, vincoli esterni o altri criteri qualitativi.

Trade-off non eliminabili

Riprendiamo un esempio concreto per mostrare cosa succede quando due vini sono incomparabili:

# Prendiamo due nodi incomparabili tra loro
id1, id2 = incomparable_pairs[0]
print(f"Confronto tra i vini {id1} e {id2}:")

v1 = df_norm.loc[id1, features]
v2 = df_norm.loc[id2, features]

comparison_df = pd.DataFrame({'Vino A': v1, 'Vino B': v2})
comparison_df['Dominanza'] = ['A > B' if a > b else ('A < B' if a < b else '=') for a, b in zip(v1, v2)]

print(comparison_df)

>>>
Confronto tra i vini 0 e 1:
                   Vino A    Vino B Dominanza
alcohol          0.842105  0.571053     A > B
malic_acid       0.191700  0.205534     A < B
color_intensity  0.372014  0.264505     A > B

Questo output mostra chiaramente che nessuno dei due vini è superiore su tutte le dimensioni. Se usassimo un indice aggregato (come una media), uno dei due verrebbe artificialmente dichiarato “migliore”, cancellando l’informazione sul conflitto tra dimensioni.

Quando interpretare il grafo e quando no

È importante sapere che un POSET è uno strumento descrittivo, non prescrittivo. Non suggerisce una decisione automatica, ma esplicita la struttura delle relazioni tra alternative. I casi di incomparabilità non sono un limite, ma una caratteristica: rappresentano incertezza legittima, pluralità di criteri e varietà delle soluzioni.

In ambiti decisionali (policy, selezione multi-obiettivo, valutazione comparativa), questa interpretazione favorisce trasparenza e responsabilità delle scelte, evitando ranking semplificati e arbitrari.

Vantaggi e limiti

L’approccio POSET presenta una serie di vantaggi importanti rispetto agli indici sintetici tradizionali, ma non è privo di limiti. Comprenderli è essenziale per decidere quando adottare un ordinamento parziale nei progetti di analisi multidimensionale.

Vantaggi

• Trasparenza: il POSET non richiede pesi soggettivi o aggregazioni arbitrarie. Le relazioni di dominanza sono determinate esclusivamente dai dati.
• Coerenza logica: una relazione di dominanza è definita solo quando esiste superiorità su tutte le dimensioni. Questo evita confronti forzati tra elementi che eccellono in aspetti diversi.
• Robustezza: le conclusioni sono meno sensibili alla scala o trasformazione dei dati, a condizione che venga mantenuto l’ordinamento relativo delle variabili.
• Identificazione di soluzioni non dominate: i nodi massimali nel grafo rappresentano scelte ottime in senso Pareto, utili in contesti decisionali multi-obiettivo.
• Esplicitazione dell’incomparabilità: l’ordinamento parziale rende visibili i trade-off e favorisce una valutazione più realistica delle alternative.

Limiti

• Assenza di un ranking unico: in alcuni contesti (e.g., concorsi, classifiche), è richiesto un ordinamento totale. Il POSET non fornisce automaticamente un vincitore.
• Complessità computazionale: per dataset molto grandi, la costruzione della matrice di dominanza e la riduzione transitiva possono diventare onerose.
• Difficoltà comunicativa: per utenti non esperti, interpretare un grafo di Hasse può essere meno immediato rispetto a una classifica numerica.
• Dipendenza da scelte preliminari: la selezione delle variabili influenza la struttura dell’ordinamento. Una scelta sbilanciata può mascherare o esagerare l’incomparabilità.

Conclusioni

L’approccio POSET offre una prospettiva alternativa potente per l’analisi di dati multidimensionali, evitando le semplificazioni imposte dagli indici aggregati. Invece di forzare un ordinamento totale, i POSET preservano la complessità informativa, mostrando chiari casi di dominanza e incomparabilità.

Questa metodologia è particolarmente utile quando:

• gli indicatori descrivono aspetti diversi e potenzialmente conflittuali (es. efficienza vs equità);
• si vogliono esplorare soluzioni non dominate, in ottica Pareto;
• è necessario garantire trasparenza nel processo decisionale.

Tuttavia, non è sempre la scelta migliore. In contesti in cui è richiesta una classifica univoca o decisioni automatizzate, può risultare meno pratica.

L’uso dei POSET dovrebbe essere considerato come una fase esplorativa o strumento complementare a metodi aggregativi, per identificare ambiguità, cluster non comparabili, e alternative equivalenti.