Tabella dei Contenuti
- Come funziona l'algoritmo K-Means
- Come trovare il numero ottimale di K con il grafico a gomito (elbow plot)
- Valutare la qualità dei cluster con il Silhouette Score
- K‑Means vs altri algoritmi di clustering
- I parametri fondamentali di K‑Means
- Caso d'uso: segmentazione dei clienti
- Rappresentazione dei gruppi avanzata
- Interpretazione del dato
- Conclusione
L'apprendimento non supervisionato è una branca fondamentale dell'analisi dei dati che si concentra sulla scoperta di strutture nascoste nei dati senza la presenza di etichette di output.
Tra le diverse tecniche di apprendimento non supervisionato, l'algoritmo K-Means è uno dei più utilizzati e apprezzati per il clustering dei dati.
Nel presente articolo, esploreremo in dettaglio il funzionamento e l'applicazione di K-means, un algoritmo di clustering partizionale che ha dimostrato di essere efficace nella suddivisione dei dati in gruppi omogenei.
Partizionale significa che, a ogni passo, lavora su una porzione diversa di dati. Questo lo differenzia dai metodi gerarchici che invece trovano nuovi cluster basandosi su cluster precedentemente stabiliti.
L'obiettivo di K-means è assegnare ogni punto dati al cluster più vicino rispetto al centroide di quel cluster, al fine di minimizzare l'errore quadratico totale.
- come funziona l'algoritmo K-Means, comprendendo l'intuizione alla sua base
- come applicarlo in Python con Sklearn
- come valutare i risultati della sua applicazione
Come funziona l'algoritmo K-Means
Il processo di raggruppamento non supervisionato può essere descritto in cinque step:
- Gli elementi del campione vengono assegnati casualmente ai K cluster definiti inizialmente. Ricordiamoci che il K-Means necessita che l'utente definisca K come iperparametro.
- Per ogni elemento del campione, viene calcolata la distanza tra esso e tutti i centroidi di classe, che rappresentano i punti medi dei cluster.
- Successivamente, ogni elemento del campione viene assegnato al cluster il cui centroide è più vicino.
- I centroidi vengono ricalcolati in base ai punti assegnati a ciascun cluster, rappresentando nuovi punti medi.
- Il processo di assegnazione e ricalcolo viene ripetuto fino a quando non si verifica la convergenza, ovvero fino a quando non ci sono ulteriori spostamenti di elementi dai cluster.
La domanda di come trovare i valore di K è legittima.
Come menzionato, K è un parametro in input al K-Means e il suo valore può cambiare completamente il comportamento di clustering.
Un metodo comune per determinare il valore di K è utilizzare il grafico a gomito (elbow plot), che mostra l'andamento dell'errore quadratico totale al variare di K.
Come trovare il numero ottimale di K con il grafico a gomito (elbow plot)
Una delle sfide principali nel clustering con K‑Means è la scelta del numero ottimale di cluster K. Il metodo più intuitivo e comunemente utilizzato è la creazione di un grafico a gomito (elbow plot)
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
# Genera un dataset fittizio
X, _ = make_blobs(n_samples=300, centers=4, cluster_std=0.6, random_state=0)
# Range di K da testare
K_range = range(1, 11)
inertia_values = []
for k in K_range:
kmeans = KMeans(n_clusters=k, init='k-means++', random_state=42)
kmeans.fit(X)
inertia_values.append(kmeans.inertia_)
# Traccia il grafico
plt.figure(figsize=(8, 5))
plt.plot(K_range, inertia_values, marker='o')
plt.xlabel('Numero di cluster K')
plt.ylabel('Inertia')
plt.title('Metodo del gomito per determinare K')
plt.grid(True)
plt.show()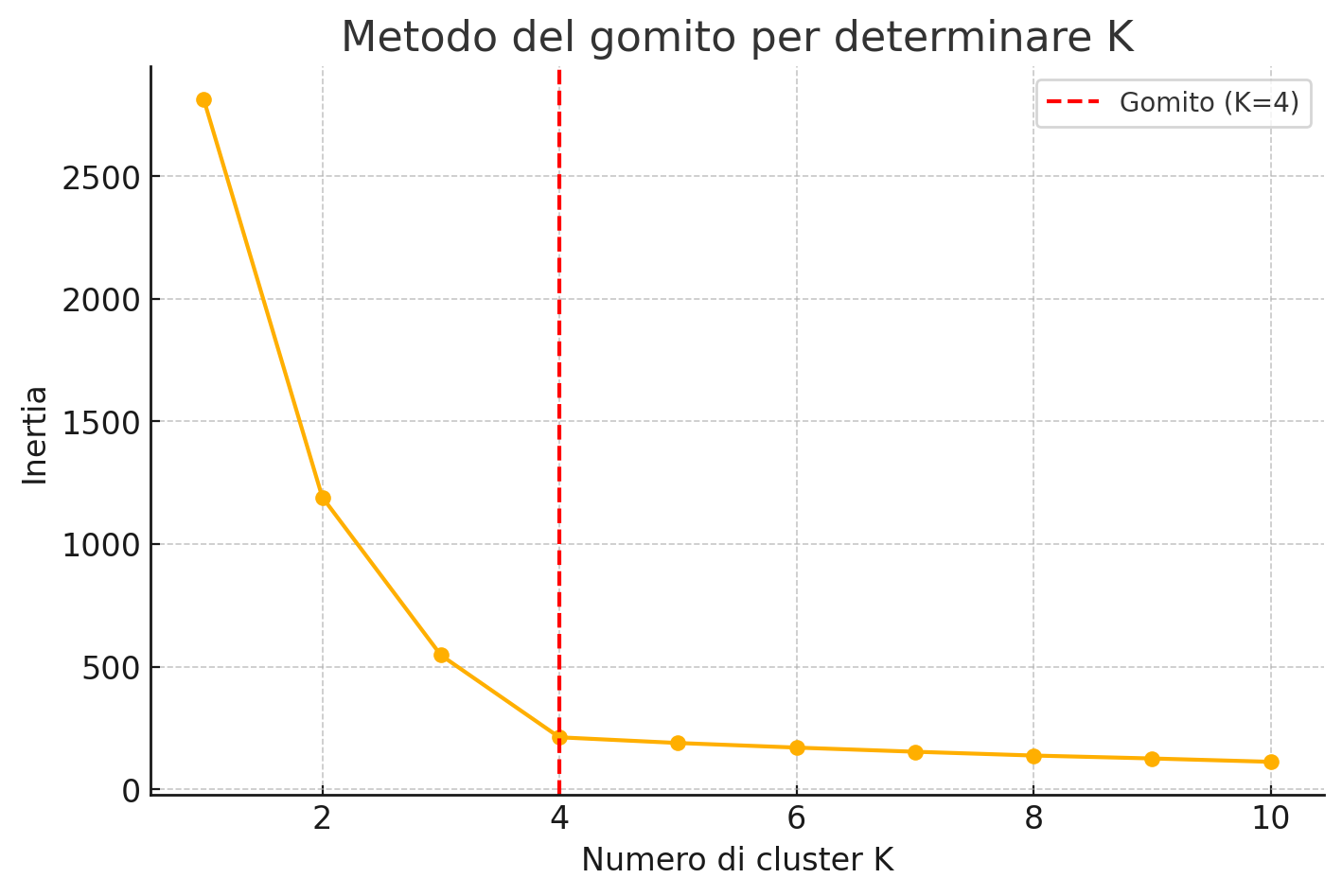
Il principio si basa sulla metrica inertia (o within-cluster sum of squares), che misura quanto i punti sono vicini al centroide del proprio cluster: valori più bassi indicano una migliore coesione interna. Tuttavia, aumentando K, l’inertia tende sempre a diminuire. L'obiettivo è trovare un punto oltre il quale l'aggiunta di un nuovo cluster non porta un miglioramento significativo. Questo punto è chiamato “gomito”.
Nei prossimi paragrafi vedremo insieme un esempio pratico segmentazione dei clienti, un caso di utilizzo classico del clustering.
Valutare la qualità dei cluster con il Silhouette Score
Il Silhouette Score è una metrica molto utilizzata per valutare la qualità di un clustering, indipendentemente dal valore di K scelto. A differenza dell’inertia, che misura la compattezza dei cluster, il Silhouette Score tiene conto anche della separazione tra cluster, fornendo una visione più equilibrata dell’efficacia della segmentazione.
Per ogni punto, il Silhouette Score confronta due quantità:
- \( a \): la distanza media tra un punto e tutti gli altri punti del suo stesso cluster (coesione).
- \( b \): la distanza media tra un punto e tutti i punti del cluster più vicino (separazione).
Il punteggio per ciascun punto si calcola con la formula:
\[ s = \frac{b-a}{max(a,b)} \]
Il risultato varia tra -1 e 1:
- valori vicini a 1 indicano che il punto è ben assegnato al suo cluster;
- valori vicini a 0 indicano che il punto è sul bordo tra due cluster;
- valori negativi suggeriscono che il punto potrebbe essere assegnato al cluster sbagliato.
Il Silhouette Score globale è la media dei punteggi di tutti i punti.
È molto facile implementare il Silhouette Score attraverso Sklearn:
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
# Definisci K
k = 3
kmeans = KMeans(n_clusters=k, init='k-means++', random_state=42)
labels = kmeans.fit_predict(X)
# Calcola il punteggio silhouette
score = silhouette_score(X, labels)
print(f"Silhouette Score per K={k}: {score:.3f}")
Un valore medio superiore a 0.5 è generalmente considerato buono, mentre un valore vicino a 1 indica una chiara separazione tra cluster. Testare diversi valori di K e confrontare i rispettivi Silhouette Score può aiutare a individuare la configurazione ottimale per il tuo dataset.
K‑Means vs altri algoritmi di clustering
Sebbene K‑Means sia uno degli algoritmi di clustering più diffusi per la sua semplicità e velocità, non è sempre la scelta migliore a causa della sua pesantezza e lentezza nell'adattarsi ad una mole di dati grande.
Infatti, K‑Means ha una complessità computazionale \( O (n \cdot{k} \cdot{i} \cdot{d}) \) dove \( n \) è il numero di campioni, \( k \) i cluster, \( i \) le iterazioni e \( d \) le dimensioni), quindi su dataset molto grandi può risultare computazionalmente costoso, soprattutto senza ottimizzazioni.
Alcuni degli algoritmi di clustering più usati oltre al K-Means includono DBSCAN, il clustering gerarchico / agglomerativo, e varianti del K-Means come K-Medoids
| Caratteristica | K‑Means | DBSCAN | Agglomerativo | K‑Medoids |
|---|---|---|---|---|
| Numero di cluster richiesto | ✅ Sì | ❌ No | ❌ No (ma può essere forzato) | ✅ Sì |
| Forma dei cluster | 🔵 Sferici | 🔶 Arbitraria | 🔷 Arbitraria | 🔵 Sferici (più flessibile) |
| Gestione outlier | ❌ Scarsa | ✅ Ottima | ❌ Limitata | ✅ Robusta |
| Sensibile a scaling? | ✅ Sì | ✅ Sì | ✅ Sì | ✅ Sì |
| Prestazioni su dataset grandi | ⚠️ Discrete (ottimizzabili) | ⚠️ Dipende da densità e dimensioni | ❌ Scarse | ❌ Scarse |
| Interpretabilità | ✅ Alta | ✅ Media | ✅ Alta | ✅ Alta |
| Visualizzazione semplice | ✅ Sì | ❌ Difficile su molti cluster | ✅ Tramite dendrogramma | ✅ Sì |
| Robustezza a centroidi iniziali | ❌ No | ✅ N/A | ✅ N/A | ✅ Più robusto |
| Parametri critici | n_clusters, init, n_init |
eps, min_samples |
Metodo di linkage | n_clusters, init, metric |
| Uso ideale | Cluster compatti e bilanciati | Cluster irregolari con rumore | Cluster gerarchici, piccoli dataset | Dataset con outlier o dati discreti |
Puoi leggere di più sugli algoritmi di clustering a questo articolo

oppure riferirti alla scheda tecnica di Sklearn dedicata.
I parametri fondamentali di K‑Means
Quando si utilizza KMeans di Scikit-Learn, è importante comprendere e configurare correttamente alcuni parametri chiave. Una buona scelta dei parametri può influenzare sia la stabilità dei risultati che i tempi di calcolo.
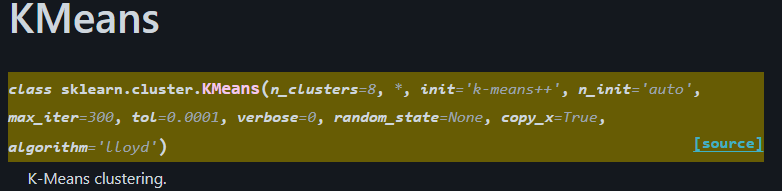
Vediamoli uno ad uno per capire cosa significano.
n_clusters
(int, default=8)
Specifica il numero di cluster K da formare. È il parametro centrale su cui si basa l’algoritmoinit
(‘k-means++’, ‘random’, array o callable)- k‑means++: initializes centroids in modo intelligente per accelerare la convergenza e migliorare la qualità finale
- random: posiziona casualmente K centri all’inizio
- Oppure puoi fornire inizializzazioni personalizzate tramite array o funzione
n_init
(‘auto’ o int, default='auto')
Numero di esecuzioni dell’algoritmo con diversi seed di inizializzazione; il modello con inertia più bassa viene scelto.- Con
init='k-means++','auto'è equivalente a1 - Con
init='random', l’impostazione predefinita è10
- Con
max_iter
(int, default=300)
Limite massimo di iterazioni per singola esecuzione. Bloccando questo parametro, possiamo controllare il tempo di calcolo garantendo comunque la convergenzatol
(float, default=1e-4)
Tolleranza relativa sulla variazione dei centroidi: quando il cambiamento è inferiore a tol, l'algoritmo si considera convergentealgorithm
(‘lloyd’ o ‘elkan’, default='lloyd')- lloyd: algoritmo standard
- elkan: più efficiente per cluster ben separati, grazie alla disuguaglianza triangolare (ma usa più memoria)
Caso d'uso: segmentazione dei clienti
Prima di tutto vediamo il dataset che ci terrà compagnia durante la lettura.
Il dataset Mall Customer, noto anche come dataset di segmentazione dei clienti, fornisce informazioni preziose sui clienti presenti in un centro commerciale.
Il dataset contiene le seguenti caratteristiche:
CustomerID: Un identificatore unico per ciascun cliente.Gender: Il genere del cliente ( Maschio o Femmina).Age: L'età del cliente.Annual Income (k$): Il reddito annuale del cliente in migliaia di dollari.Spending Score (1-100): Un punteggio assegnato a ciascun cliente in base al loro comportamento di spesa e altre caratteristiche legate agli acquisti.
L'obiettivo dell'analisi del dataset in questione è quello di eseguire la segmentazione dei clienti, ovvero suddividere i clienti in gruppi distinti in base alle loro caratteristiche simili.
La segmentazione dei clienti aiuta le aziende a identificare segmenti di clientela preziosi, comprendere le loro esigenze e sviluppare strategie di marketing personalizzate per raggiungere ciascun segmento in modo efficace.
Utilizzando vari algoritmi di clustering come K-Means, le aziende possono identificare modelli e preferenze tra i diversi gruppi di clienti.
Questa segmentazione consente alle aziende di offrire promozioni mirate, creare raccomandazioni di prodotti personalizzati e ottimizzare la disposizione dei negozi per migliorare l'esperienza del cliente.
Iniziamo a vedere gli import
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import plotly as ply
import plotly.express as px
import plotly.graph_objs as go
from plotly.subplots import make_subplots
import plotly.subplots as sp
from sklearn.cluster import KMeans
df = pd.read_csv("/content/drive/MyDrive/Colab Notebooks/Mall_Customers.csv")
df.head()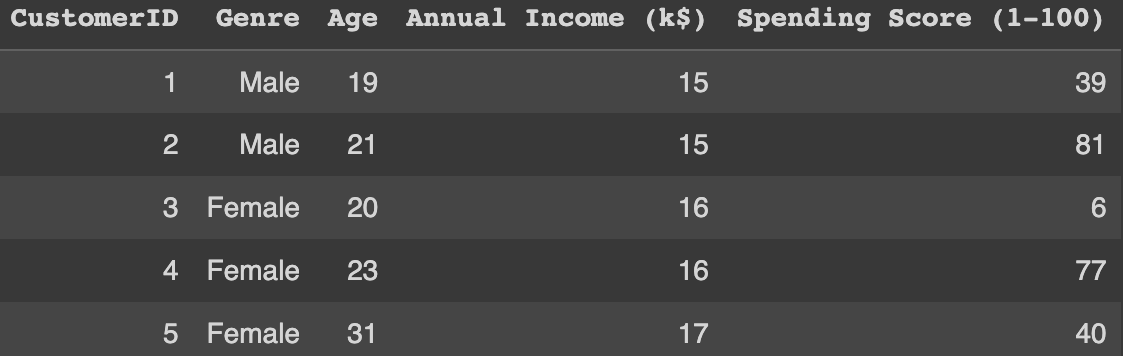
È composto da 200 osservazioni di cui distinguiamo 112 Donne e 88 Uomini.
sns.countplot(y = 'Gender', data = df)
plt.show()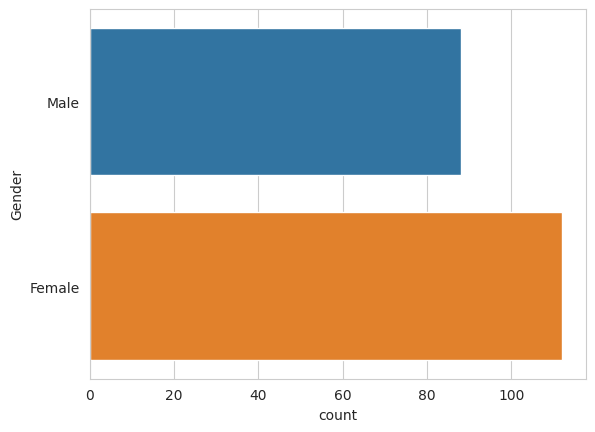
Grazie a Seaborn possiamo creare efficacemente grafici che vengono divisi per una variabile specifica. In questo caso, genere.
df.drop(['CustomerID'], axis = 1, inplace = True)
sns.pairplot(df, hue = 'Gender')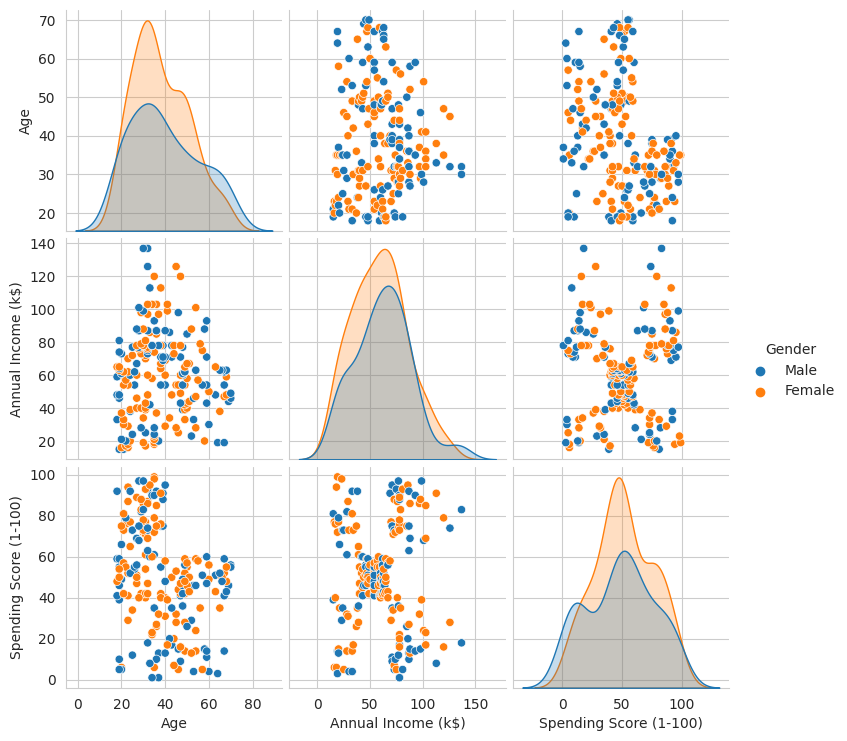
Viene creato un grafico con una griglia di grafici di dispersione (scatter plot). Sulla diagonale principale della griglia, troviamo le densità delle distribuzioni delle variabili condizionatamente al genere.
Negli altri pannelli della griglia, abbiamo gli scatter plot per le coppie di variabili, consentendo di esplorare le relazioni tra di esse in modo rapido ed efficace.
from sklearn.preprocessing import StandardScaler
X1 = df.loc[:,['Age', 'Spending Score (1-100)']].values
X2 = df.loc[:,['Annual Income (k$)', 'Spending Score (1-100)']].values
X3 = df.loc[:,['Age', 'Annual Income (k$)']].values
# Standardizziamo i dati
scaler = StandardScaler()
X1 = scaler.fit_transform(X1)
X2 = scaler.fit_transform(X2)
X3 = scaler.fit_transform(X3)Applichiamo la standardizzazione ai dati poi X1, X2, X3 sono tre diverse combinazioni di feature prese dal DataFrame. Ogni variabile X rappresenta una diversa combinazione di due colonne del DataFrame.
Ora creiamo un grafico a gomito.
sse = []
k_rng = range(1,10) # numero di cluster testati
for k in k_rng:
km1 = KMeans(n_clusters=k)
km1.fit(X1)
sse.append(km1.inertia_)
# SSE per tutti i punti dati nel dataset rispetto ai centroidi dei cluster a cui sono stati assegnati.
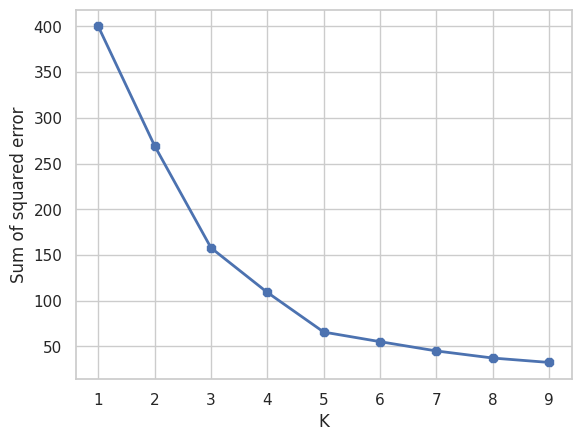
Calcoliamo la somma degli errori quadratici (SSE) per diverse configurazioni del numero di cluster utilizzando l'algoritmo K-means su dati standardizzati. Alla fine del loop, avremo una lista contenente i valori SSE per ciascun numero di cluster testato su X1.
Questi valori possono essere utilizzati per tracciare il grafico a gomito (elbow plot) e identificare il numero ottimale di cluster per i dati.
Di fatto, il grafico a gomito mostra come la somma degli SSE cambia all'aumentare di K. Il valore più basso dove la diminuzione del SSE non è repentina viene considerato come gomito, cioè numero di K.
plt.xlabel('K')
plt.ylabel('Sum of squared error')
plt.plot(k_rng,sse, linewidth=2, marker='8')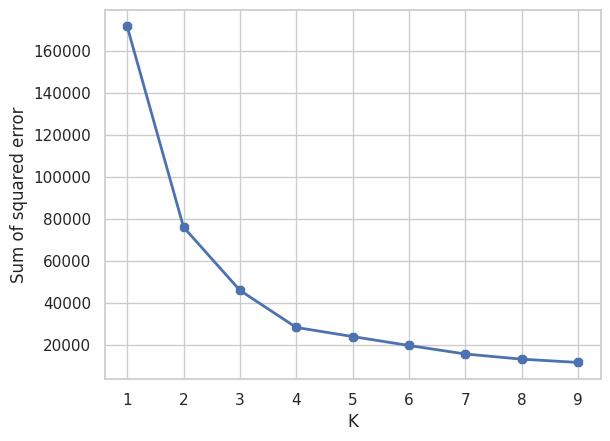
Vediamo come il valore ottimale è K = 4 poiché dopo il 4 il valore del SSE diminuisce più lentamente.
A questo punto implementiamo l'algoritmo K-means.
km1 = KMeans(n_clusters=4)
y_predicted1 = km1.fit_predict(X1)
y_predicted1L'array y_predicted1 contiene le etichette dei cluster per i dati X1 in base all'algoritmo K-means con 4 cluster. Ogni elemento dell'array rappresenta il cluster assegnato per il corrispondente punto dati in X1.
plt.scatter(X1[:,0],X1[:,1],c=km1.labels_, cmap='rainbow')
plt.scatter(km1.cluster_centers_[:,0],km1.cluster_centers_[:,1], color='black', marker='*', label='centroid')
plt.xlabel('Age (scaled)')
plt.ylabel('Spending Score (scaled)')
plt.legend()
plt.show()
plt.show()
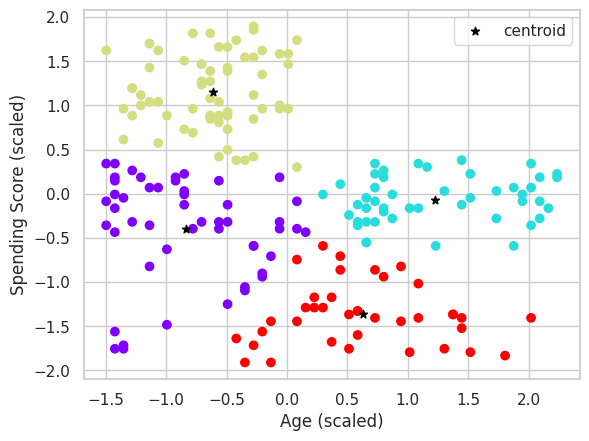
Visualizziamo i risultati del clustering ottenuti dall'algoritmo K-Means sui dati standardizzati X1.
Il grafico mostra i punti dati nel piano bidimensionale delle feature Age e Spending Score (1-100) colorati in base all'etichetta del cluster assegnata loro dall'algoritmo K-Means, e i centroidi dei cluster saranno rappresentati da stelle nere.
In questi casi, i gruppi possono essere creati sul risultato della PCA, avendo quindi una rappresentazione di tutte le feature (X1, X2, ..., etc).
Rappresentazione dei gruppi avanzata
Adesso non resta che ripetere la procedura per le altre due configurazioni di dati X2 e X3.
Useremo però una modalità di visualizzazione più chiara usando una funzione helper con Sklearn.
kmeans_kwargs = {
'init': 'k-means++', #inizializzazione uniforme dei centroidi
'n_init': 20, # numero di inizializzazioni diverse
'max_iter': 300,
'random_state': 42
}Definiamo un dizionario kmeans_kwargs contenente diversi parametri da utilizzare nell'algoritmo K-Means. Questi parametri possono essere passati come argomenti per personalizzare il comportamento dell'algoritmo K-means.
Machine Learning Engineering
Andriy Burkov
Questo è IL libro di IA applicata più completo in circolazione. È pieno di best practice e modelli di progettazione per la creazione di soluzioni di apprendimento automatico affidabili e scalabili.
Questi parametri sono opzionali e possono essere utilizzati per ottimizzare le prestazioni dell'algoritmo in base alle caratteristiche specifiche del dataset.
def kmeans_model(k, x): #k = cluster x = dati
model = KMeans(k, **kmeans_kwargs)
model.fit(x)
labels = model.labels_
centroids = model.cluster_centers_
return model, labels, centroidsdef plot_clusters(x, h, model, labels, centroids):
# meshgrid
x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1
y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
z = model.predict(np.c_[xx.ravel(), yy.ravel()])
z = z.reshape(xx.shape) #stessa dimensione meshgrid
# rappresentazione cluster con meshgrid
sns.set_style('ticks')
plt.clf()
plt.figure(figsize=(12, 6))
plt.imshow(z, interpolation = 'nearest',
extent = (xx.min(), xx.max(), yy.min(), yy.max()),
cmap = 'Pastel1', aspect = 'auto',
origin = 'lower')
sns.scatterplot(x = x[:, 0], y = x[:, 1],
hue = labels, palette = 'tab10', s = 100)
plt.scatter(x = centroids[:, 0] , y = centroids[:, 1],
s = 100, c = 'black', alpha = 0.8, marker = 'X')
plt.xlim(x_min, x_max)
plt.ylim(y_min, y_max)
plt.show()
Creiamo una funzione per un grafico utile a visualizzare la suddivisione del piano bidimensionale in cluster e i centroidi dei cluster.
Viene utilizzato meshgrid per creare una griglia di punti in tutto lo spazio dei dati, e per ciascun punto del meshgrid, viene previsto il cluster a cui appartiene utilizzando il modello K-Means addestrato.
In seguito, i punti dati sono colorati in base alle etichette dei cluster, i centroidi dei cluster sono rappresentati come simboli "X" neri.
X2_model, X2_labels, X2_centroids = kmeans_model(5, X2)
plot_clusters(X2, 0.02, X2_model, X2_labels, X2_centroids)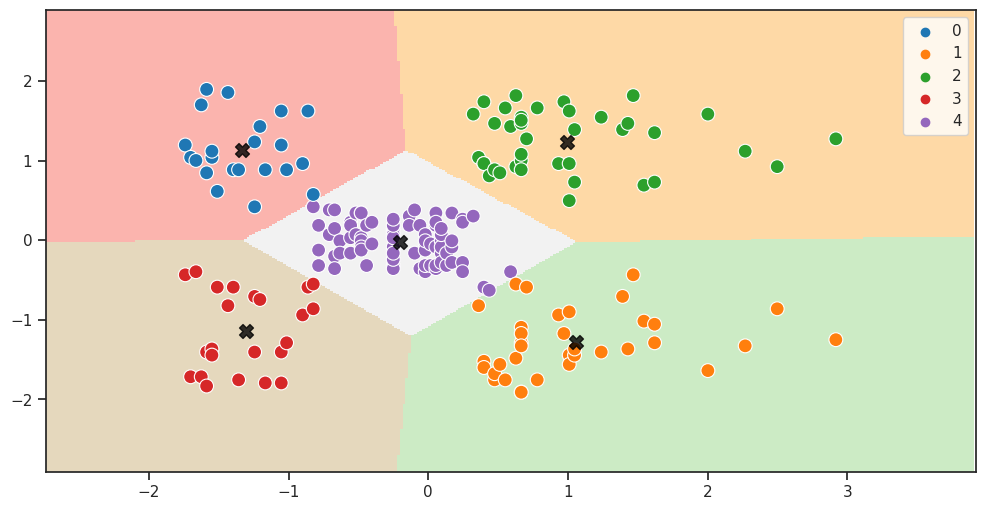
Visualizziamo i risultati del clustering ottenuti dall'algoritmo K-Means sui dati standardizzati X2.
Il grafico mostra i punti dati nel piano bidimensionale delle feature Annual Income (k$) e Spending Score (1-100) colorati in base all'etichetta del cluster assegnata loro dall'algoritmo K-Means, e i centroidi dei cluster saranno rappresentati da stelle nere.
Per questa configurazioni di dati il valore di K è 5.
X3_model, X3_labels, X3_centroids = kmeans_model(3, X3)
plot_clusters(X3, 0.02, X3_model, X3_labels, X3_centroids)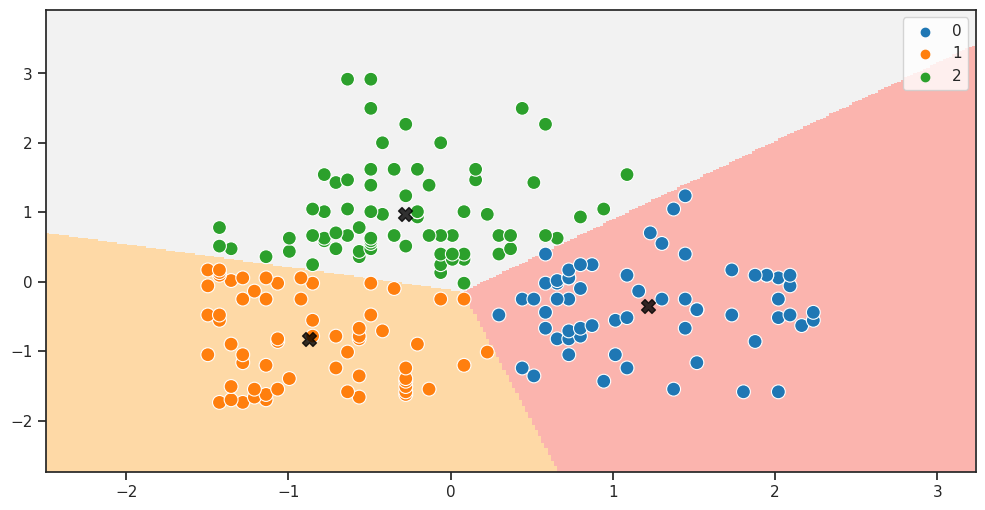
Visualizziamo i risultati del clustering ottenuti dall'algoritmo K-Means sui dati standardizzati X2.
Il grafico mostra i punti dati nel piano bidimensionale delle feature Age e Annual Income (k$) colorati in base all'etichetta del cluster assegnata loro dall'algoritmo K-Means, e i centroidi dei cluster saranno rappresentati da stelle nere.
Interpretazione del dato
La segmentazione vista sopra è molto rilevante per il business.
Questo perché gruppi diversi hanno comportamenti diversi.
Se implementata nel nostro business, questo tipo di logica permette di collocare facilmente un utente in uno specifico gruppo di comportamenti.
Questi comportamenti possono essere poi oggetto di campagne di marketing oppure di strategie dedicate.
Conclusione
La tecnica di clustering K-Means è un algoritmo di apprendimento non supervisionato ampiamente utilizzato nella data science per identificare strutture nascoste nei dati e suddividerli in gruppi omogenei.
Ha diversi pregi e difetti che devono essere considerati quando si applica questa tecnica.
Pregi del K-Means
- Semplice da implementare e veloce: K-Means è un algoritmo semplice e intuitivo da implementare, rendendolo ideale per la rapida analisi esplorativa dei dati.
- Scalabilità: K-Means funziona bene su dataset con un gran numero di punti dati e feature. Può essere utilizzato anche con dati di alta dimensionalità senza compromettere significativamente le prestazioni.
- Interpretabilità dei risultati: I cluster creati da K-Means sono facilmente interpretabili, poiché ogni cluster è rappresentato da un centroide e le istanze più vicine a quel centroide appartengono a quel cluster. Ciò facilita la comprensione delle strutture nascoste nei dati.
- Adattabilità: K-Means è flessibile e può essere facilmente adattato per affrontare diverse sfide di clustering. È possibile scegliere il numero di cluster desiderato e personalizzare i parametri per ottenere i risultati desiderati.
Difetti del K-Means
- Numero di cluster predefinito: L'utente deve specificare il numero di cluster desiderato (K) prima dell'esecuzione dell'algoritmo. Tuttavia, scegliere il numero ottimale di cluster può essere un'attività soggettiva e talvolta difficile.
- Sensibile all'inizializzazione dei centroidi: L'output di K-means può variare a seconda dell'inizializzazione casuale dei centroidi dei cluster. Ciò può portare a risultati diversi in esecuzioni multiple.
- Non adatto a forme di cluster complesse: K-Means fa l'assunzione che i cluster siano di forma sferica e con la stessa varianza. Pertanto, potrebbe non funzionare bene con cluster di forma irregolare o di dimensioni diverse.
- Sensibile alla normalizzazione delle feature: K-Means è influenzato dalla scala delle feature presenti nel dataset. Pertanto, è fondamentale standardizzare i dati prima di eseguire l'algoritmo per garantire che tutte le feature abbiano lo stesso impatto.
- Computazionalmente oneroso: se il dataset è molto grande (già 100k+ righe) oppure pieno di feature, il K-Means potrebbe non essere la soluzione ideale per il clustering, in quanto la convergenza sarebbe molto lenta.
K-Means rimane uno strumento prezioso. Nella pratica, è sempre consigliabile eseguire diverse prove con valori diversi di K e considerare l'uso di altre tecniche di clustering per affrontare le limitazioni di K-Means in caso di strutture di cluster più complesse.








Commenti dalla community